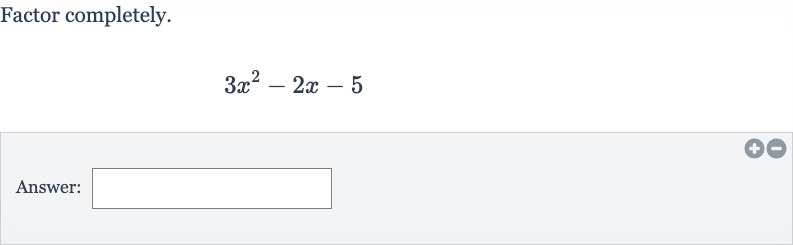
Factor completely. 3x^(2)-2x-5 Answer:

Question

Factor completely.  3x^(2)-2x-5 Answer:

Bytelearn · Accepted Answer

Identify Coefficients: Identify the coefficients of the quadratic expression. The quadratic expression is 3x^2 - 2x - 5. Here, the coefficient of x^2 (a) is 3, the coefficient of x (b) is -2, and the constant term (c) is -5.Determine Factoring Feasibility: Determine if the quadratic expression can be factored using simple factoring techniques. Since the coefficient of x^2 is not 1, we need to find two numbers that multiply to ac (3 * -5 = -15) and add up to b (-2). We are looking for two numbers that multiply to -15 and add up to -2.Find Suitable Numbers: Find two numbers that meet the criteria. After checking possible pairs of factors of -15, we find that there are no two integers that multiply to -15 and add up to -2. Therefore, we cannot factor this quadratic expression using simple factoring techniques.Use Quadratic Formula: Use the quadratic formula to check if the expression can be factored over the real numbers. The quadratic formula is x = [-b ± sqrt(b^2 - 4ac)] / (2a). For our expression, a = 3, b = -2, and c = -5. Let's calculate the discriminant (b^2 - 4ac) to see if the roots are real numbers. Discriminant = (-2)^2 - 4(3)(-5) = 4 + 60 = 64. Since the discriminant is positive, we have two distinct real roots.Calculate Roots: Calculate the roots using the quadratic formula. x = [-(-2) ± sqrt(64)] / (2 * 3) x = [2 ± 8] / 6 We have two roots: x = (2 + 8) / 6 and x = (2 - 8) / 6 x = 10 / 6 and x = -6 / 6 x = 5 / 3 and x = -1Write Factored Form: Write the factored form using the roots. The factored form of the quadratic expression is (3x - 5)(x + 1).

Factor completely. $\newline$ $3 x^{2}-2 x-5$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline3x2−2x−5 3 x^{2}-2 x-5 3x2−2x−5\newlineAnswer:

Factor completely. $\newline$ $3 x^{2}-2 x-5$ $\newline$ Answer: