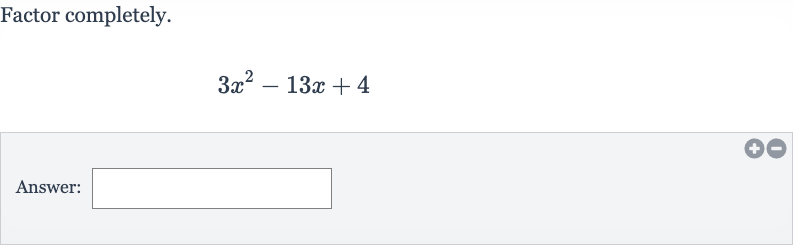
Factor completely. 3x^(2)-13 x+4 Answer:

Question

Factor completely.  3x^(2)-13 x+4 Answer:

Bytelearn · Accepted Answer

Identify a, b, c: Identify a, b, and c in the quadratic expression 3x^2 - 13x + 4. Compare 3x^2 - 13x + 4 with ax^2 + bx + c. a = 3 b = -13 c = 4Find product and sum: Find two numbers whose product is a*c (3*4 = 12) and whose sum is b (-13). We need to find two numbers that multiply to 12 and add up to -13. After checking possible pairs of factors of 12 (1 and 12, 2 and 6, 3 and 4), we find that none of these pairs add up to -13. This means we need to consider negative factors because the sum is negative and the product is positive. The correct pair of numbers that satisfy these conditions are -1 and -12. -1 * -12 = 12 -1 + -12 = -13Rewrite middle term: Rewrite the middle term -13x using the two numbers found in Step 2. 3x^2 - 13x + 4 becomes 3x^2 - 1x - 12x + 4.Factor by grouping: Factor by grouping. Group the terms: (3x^2 - 1x) and (-12x + 4). Factor out the greatest common factor from each group. From the first group, we can factor out an x: x(3x - 1). From the second group, we can factor out a -4: -4(3x - 1).Factor common binomial: Factor out the common binomial factor. We now have x(3x - 1) - 4(3x - 1). The common binomial factor is (3x - 1). Factor this out to get (3x - 1)(x - 4).

Factor completely. $\newline$ $3 x^{2}-13 x+4$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline3x2−13x+4 3 x^{2}-13 x+4 3x2−13x+4\newlineAnswer:

Factor completely. $\newline$ $3 x^{2}-13 x+4$ $\newline$ Answer: