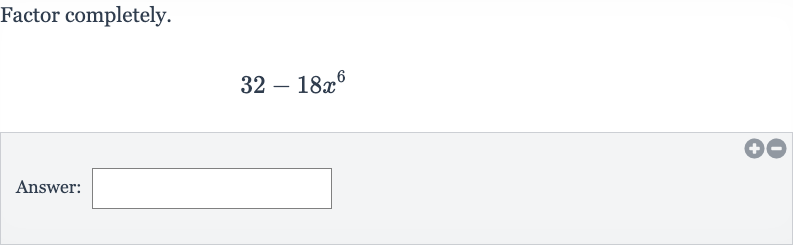
Factor completely. 32-18x^(6) Answer:

Question

Factor completely.  32-18x^(6) Answer:

Bytelearn · Accepted Answer

Identify GCF: Identify the greatest common factor (GCF) of the terms 32 and -18x^(6). The GCF of 32 and 18 is 2. Since there is an x term in one of the terms, and it is to the power of 6, we can take x^6 as a common factor as well. However, since there is no x term in 32, we cannot take x as a common factor. The GCF is therefore 2.Factor out GCF: Factor out the GCF from the expression 32 - 18x^(6). This gives us 2(16 - 9x^(6)).Recognize difference of squares: Recognize that 16 - 9x^(6) is a difference of squares, since 16 is 4^2 and 9x^(6) is (3x^(3))^2. The difference of squares can be factored as (a^2 - b^2) = (a - b)(a + b). Here, a = 4 and b = 3x^(3).Apply difference of squares formula: Apply the difference of squares formula to factor 16 - 9x^(6). This gives us (4 - 3x^(3))(4 + 3x^(3)).Combine factored forms: Combine the factored form of the difference of squares with the GCF that was factored out earlier. The final factored form is 2(4 - 3x^(3))(4 + 3x^(3)).

Factor completely. $\newline$ $32-18 x^{6}$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline32−18x6 32-18 x^{6} 32−18x6\newlineAnswer:

Factor completely. $\newline$ $32-18 x^{6}$ $\newline$ Answer: