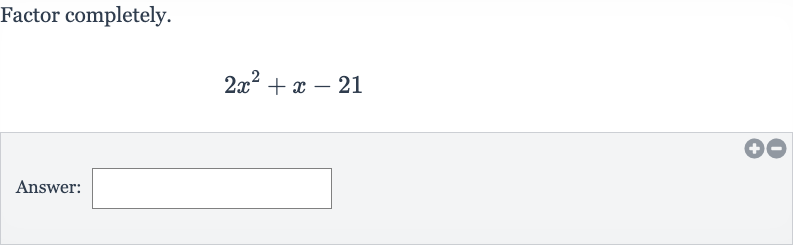
Factor completely. 2x^(2)+x-21 Answer:

Question

Factor completely.  2x^(2)+x-21 Answer:

Bytelearn · Accepted Answer

Identify Coefficients: Step Title: Identify the Coefficients Concise Step Description: Identify the coefficients of the quadratic equation, which are the numbers in front of the variables. In this case, the coefficients are 2, 1, and -21. Step Calculation: Coefficients are 2, 1, -21 Step Output: Coefficients: 2, 1, -21Find Factors: Step Title: Find the Factors Concise Step Description: Find two numbers that multiply to the product of the first and last coefficients (2 * -21 = -42) and add to the middle coefficient (1). Step Calculation: Factors of -42 that add up to 1 are 7 and -6 (because 7 * -6 = -42 and 7 + (-6) = 1). Step Output: Factors: 7, -6Rewrite Middle Term: Step Title: Rewrite the Middle Term Concise Step Description: Rewrite the middle term using the factors found in the previous step. Step Calculation: The quadratic equation can be rewritten as 2x^2 + 7x - 6x - 21. Step Output: Rewritten Quadratic: 2x^2 + 7x - 6x - 21Factor by Grouping: Step Title: Factor by Grouping Concise Step Description: Group the terms into two pairs and factor out the common factors from each pair. Step Calculation: Group (2x^2 + 7x) and (-6x - 21), then factor out the common factors. From the first group, we can factor out x, and from the second group, we can factor out -3. Step Output: Factored Groups: x(2x + 7) - 3(2x + 7)Factor Out Common Binomial: Step Title: Factor Out the Common Binomial Concise Step Description: Factor out the common binomial from the two groups. Step Calculation: The common binomial is (2x + 7), so we factor it out to get the final factored form. Step Output: Factored Form: (x - 3)(2x + 7)

Factor completely. $\newline$ $2 x^{2}+x-21$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely.\newline2x2+x−21 2 x^{2}+x-21 2x2+x−21\newlineAnswer:

Factor completely. $\newline$ $2 x^{2}+x-21$ $\newline$ Answer: