AI tutor
Full solution
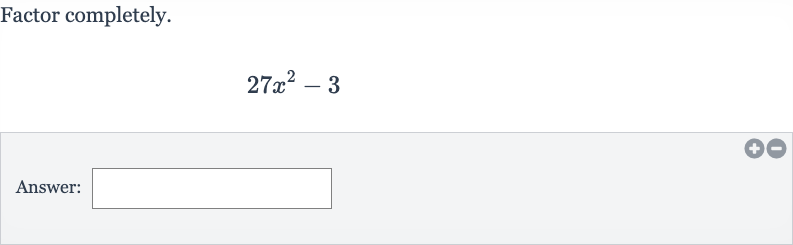
Q. Factor completely.Answer:
- Identify Form: Identify the form of the expression.The given expression is , which is a difference of squares because it can be written as .
- Apply Formula: Apply the difference of squares formula.The difference of squares formula is . Here, and .
- Factor Expression: Factor the expression using the formula.Substitute and into the formula to get .
- Check Factoring: Check the factoring. , which is not the original expression. We made a mistake in the calculation of . It should be , not . Therefore, there is a math error.