AI tutor
Full solution
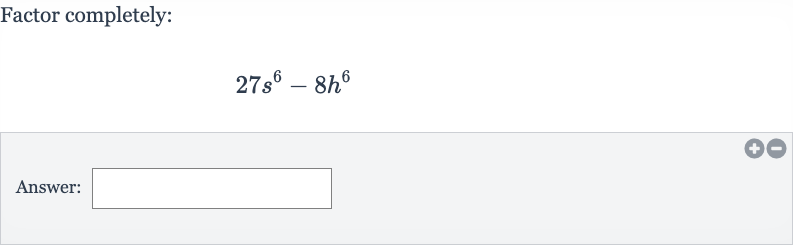
Q. Factor completely:Answer:
- Identify Expression Type: Step Title: Identify the Type of ExpressionConcise Step Description: Recognize that the expression is a difference of two cubes.Step Calculation: The expression can be rewritten as .
- Apply Cubes Formula: Step Title: Apply the Difference of Cubes FormulaConcise Step Description: Use the formula to factor the expression.Step Calculation: Let and . Then, apply the formula to get .
- Simplify Factored Expression: Step Title: Simplify the Factored ExpressionConcise Step Description: Simplify the terms inside the second set of parentheses.Step Calculation: Simplify to get .
More problems from Factor polynomials
QuestionGet tutor help
QuestionGet tutor help