AI tutor
Full solution
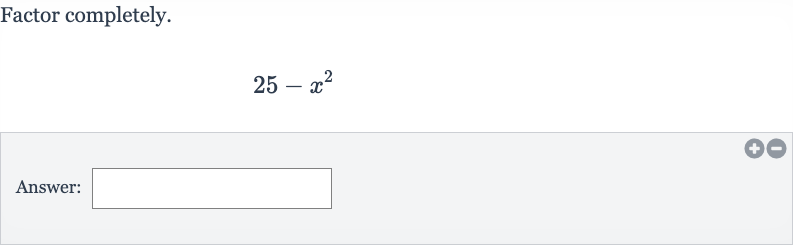
Q. Factor completely.Answer:
- Identify as difference of squares: Identify the expression as a difference of squares.The expression can be written as , where and .This means and , since and .
- Apply formula to factor: Apply the difference of squares formula to factor the expression.The difference of squares formula is .Substitute and into the formula to get .
- Write final factored form: Write the final factored form of the expression.The factored form of is .