Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Factor completely: 2(4x-3)^(4)+(4x-3)^(5) Answer:

Factor completely:\newline2(4x−3)4+(4x−3)5 2(4 x-3)^{4}+(4 x-3)^{5} \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 6right chevron icon
Factor numerical expressions using the distributive propertyright chevron icon

Full solution

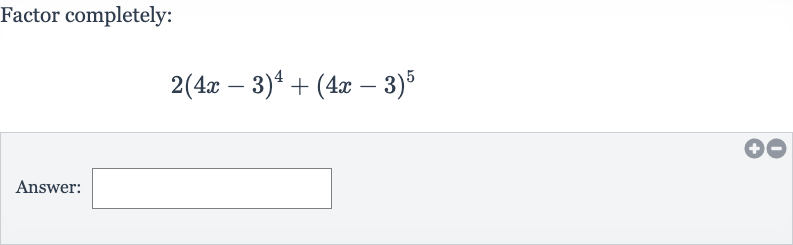
Q. Factor completely:\newline2(4x−3)4+(4x−3)5 2(4 x-3)^{4}+(4 x-3)^{5} \newlineAnswer:
  1. Identify common factor: Identify the common factor in both terms.\newlineThe common factor in both terms is (4x−3)4(4x-3)^{4} since it is present in both terms of the expression.
  2. Factor out: Factor out the common factor from the expression.\newlineWe can factor (4x−3)4(4x-3)^{4} out of both terms to get (4x−3)4(2+(4x−3))(4x-3)^{4}(2 + (4x-3)).
  3. Simplify expression: Simplify the expression inside the parentheses.\newlineSimplifying the expression inside the parentheses gives us (4x−3)4(2+4x−3)(4x-3)^{4}(2 + 4x - 3).
  4. Combine like terms: Combine like terms inside the parentheses.\newlineCombining like terms 22 and −3-3 gives us (4x−3)4(4x−1)(4x-3)^{4}(4x - 1).
  5. Write final form: Write down the final factored form.\newlineThe completely factored form of the expression is (4x−3)4(4x−1)(4x-3)^{4}(4x - 1).

More problems from Factor numerical expressions using the distributive property

Question
Simplify the expression:\newline7z2+3z27z^2 + 3z^2 \newline ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify the expression:\newline10f+8f−9f−6f10f + 8f - 9f - 6f\newline____
Get tutor helpright-arrow

Posted 1 month ago

Question
Subtract.\newline(3h+6)−(3h+2)(3h + 6) - (3h + 2)\newline____
Get tutor helpright-arrow

Posted 1 month ago

Question
Simplify the expression:\newline2p−p2p - p \newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
A school charges $6\$6 per ticket to a dance. They spend $300\$300 on music and decorations. The expression 6n−3006n-300 describes the amount of profit the school makes from the dance if nn students buy tickets. What does 6n6n represent in this context?\newlineChoices:\newline(A)The amount of money the school charges for all `\n` tickets\newline(B)The amount of money the school spends on the dance\newline(C)The number of students who buy tickets\newline(D)The profit the school earns per ticket
Get tutor helpright-arrow

Posted 2 months ago

Question
Which is equal to cos⁡60∘ \cos 60^\circ ? \newlineChoices:\newline(A) sin⁡30∘ \sin 30^\circ \newline(B) sin⁡60∘ \sin 60^\circ \newline(C) cos⁡30∘ \cos 30^\circ \newline(D) cos⁡60∘ \cos 60^\circ
Get tutor helpright-arrow

Posted 3 months ago

Question
Which is equal to sin⁡45∘\sin 45^\circ? \newlineChoices:\newline(A) cos⁡45∘\cos 45^\circ\newline(B) cos⁡55∘\cos 55^\circ\newline(C) sin⁡55∘\sin 55^\circ\newline(D) sin⁡35∘\sin 35^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Which is equal to cos⁡75∘\cos 75^\circ? \newlineChoices:\newline(A) sin⁡15∘\sin 15^\circ\newline(B) sin⁡75∘\sin 75^\circ\newline(C) cos⁡15∘\cos 15^\circ\newline(D) cos⁡25∘\cos 25^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Which is equal to sin⁡30∘ \sin 30^\circ ? \newlineChoices:\newline(A) cos⁡60∘ \cos 60^\circ \newline(B) cos⁡30∘ \cos 30^\circ \newline(C) sin⁡60∘ \sin 60^\circ \newline(D) sin⁡30∘ \sin 30^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Which is equal to cos⁡45∘ \cos 45^\circ ? \newlineChoices:\newline(A) sin⁡45∘ \sin 45^\circ \newline(B) sin⁡55∘ \sin 55^\circ \newline(C) cos⁡55∘ \cos 55^\circ \newline(D) cos⁡35∘ \cos 35^\circ
Get tutor helpright-arrow

Posted 1 month ago

View all (46)