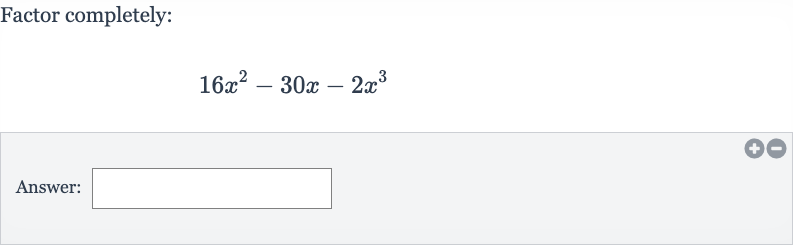
Factor completely: 16x^(2)-30 x-2x^(3) Answer:

Question

Factor completely:  16x^(2)-30 x-2x^(3) Answer:

Bytelearn · Accepted Answer

Arrange Polynomial Descending Order: Write down the polynomial and arrange it in descending order of powers of x. We have the polynomial 16x^2 - 30x - 2x^3. To arrange it in descending order, we rewrite it as -2x^3 + 16x^2 - 30x.Factor Out Greatest Common Factor: Factor out the greatest common factor (GCF) from the polynomial. The GCF of the coefficients -2, 16, and -30 is 2. However, since the leading coefficient is negative, we will factor out -2 to keep the leading term positive. We also factor out an x since all terms have at least one x. Factoring out -2x, we get -2x(x^2 - 8x + 15).Factor Quadratic Expression: Factor the quadratic expression inside the parentheses. We need to find two numbers that multiply to give the product (ac = 15) and add to give the middle coefficient (b = -8). The numbers that satisfy this are -3 and -5, since (-3) * (-5) = 15 and (-3) + (-5) = -8. So, we can factor the quadratic as (x - 3)(x - 5).Write Fully Factored Form: Write down the fully factored form of the polynomial. Combining the factored out term from Step 2 and the factored quadratic from Step 3, we get the fully factored form of the polynomial: -2x(x - 3)(x - 5).

Factor completely: $\newline$ $16 x^{2}-30 x-2 x^{3}$ $\newline$ Answer:

Full solution

More problems from Factor polynomials

Related topics

Factor completely:\newline16x2−30x−2x3 16 x^{2}-30 x-2 x^{3} 16x2−30x−2x3\newlineAnswer:

Factor completely: $\newline$ $16 x^{2}-30 x-2 x^{3}$ $\newline$ Answer: