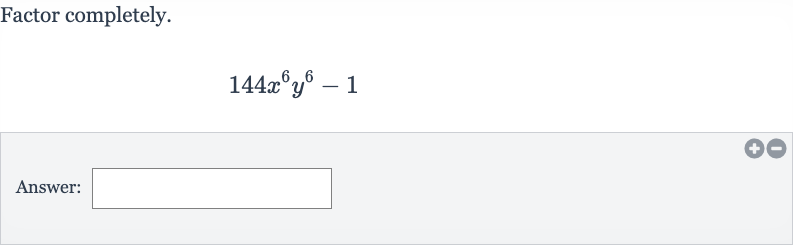AI tutor
Full solution
Q. Factor completely.Answer:
- Recognize Difference of Squares: Step Title: Recognize the Difference of SquaresConcise Step Description: Identify that the expression is a difference of squares, which can be factored into the product of two binomials.Step Calculation: Recognize that is a perfect square, as is , so the expression can be written as .Step Output: Expression as a difference of squares:
- Apply Formula for Factoring: Step Title: Apply the Difference of Squares FormulaConcise Step Description: Use the difference of squares formula to factor the expression.Step Calculation: Apply the formula with and to get .Step Output: Factored form using the difference of squares:
More problems from Factor polynomials
QuestionGet tutor help
QuestionGet tutor help