AI tutor
Full solution
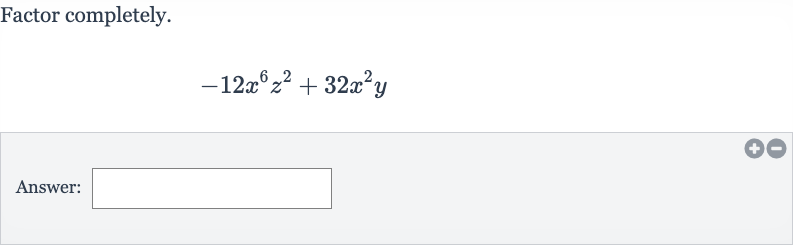
Q. Factor completely.Answer:
- Identify GCF: Identify the greatest common factor (GCF) of the terms in the expression .The GCF of and is .The GCF of and is since we take the lowest power of common to both terms.There is no common factor for and , and since one term has a and the other has a , they do not contribute to the GCF.The GCF is therefore .
- Factor Out GCF: Factor out the GCF from each term in the expression.Expression: Factored form:
- Check Further Factoring: Check if the terms inside the parentheses can be factored further.The term does not have any common factors with other than , and there are no common variables. Therefore, the terms inside the parentheses cannot be factored further.
More problems from Multiply and divide rational expressions
QuestionGet tutor help