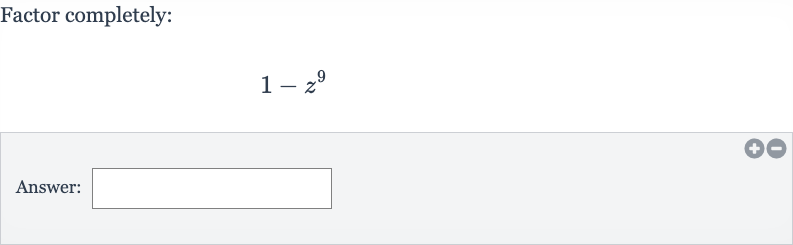
Factor completely: 1-z^(9) Answer:

Question

Factor completely:  1-z^(9) Answer:

Bytelearn · Accepted Answer

Identify Factoring Type: Identify the type of factoring required for the expression 1 - z^(9). The expression is a difference of two terms, and since one of the terms is 1, which is a perfect square (1^2), and the other term is z^(9), which can be written as (z^3)^3, we can recognize this as a difference of cubes: a^3 - b^3.Apply Difference of Cubes: Apply the difference of cubes formula to factor the expression. The difference of cubes formula is a^3 - b^3 = (a - b)(a^2 + ab + b^2). Here, a = 1 and b = z^3. So, 1 - z^(9) = (1 - z^3)(1^2 + 1*z^3 + (z^3)^2).Simplify Factored Expression: Simplify the factored expression. 1 - z^(9) = (1 - z^3)(1 + z^3 + z^6).Recognize Simplified Term: Recognize that the term 1 + z^3 + z^6 is already simplified and cannot be factored further using real numbers. The expression 1 + z^3 + z^6 does not have any common factors, nor does it fit any special factoring formulas such as difference of squares or sum/difference of cubes.Write Completely Factored Form: Write down the completely factored form of the original expression. The completely factored form of 1 - z^(9) is (1 - z^3)(1 + z^3 + z^6).

Factor completely: $\newline$ $1-z^{9}$ $\newline$ Answer:

Full solution

More problems from Factor quadratics: special cases

Related topics

Factor completely:\newline1−z9 1-z^{9} 1−z9\newlineAnswer:

Factor completely: $\newline$ $1-z^{9}$ $\newline$ Answer: