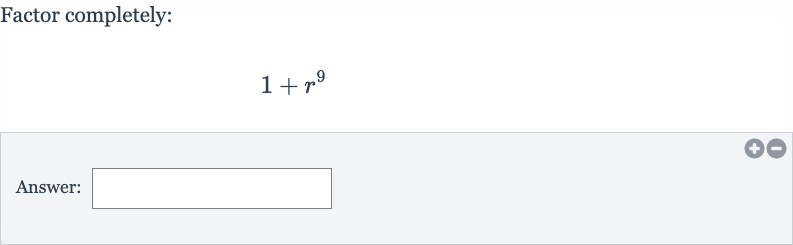
Factor completely: 1+r^(9) Answer:

Question

Factor completely:  1+r^(9) Answer:

Bytelearn · Accepted Answer

Identify Expression Type: Identify the type of expression and the possible factoring technique. The expression 1 + r^9 is a sum of two terms. One of the terms is a perfect power of r. We can consider if it's possible to apply a sum of cubes or a sum of higher powers factoring technique.Recognize Perfect Cube: Recognize that r^9 is a perfect cube, as r^9 = (r^3)^3. The expression can be rewritten as 1^3 + (r^3)^3, which resembles the sum of cubes formula a^3 + b^3 = (a + b)(a^2 - ab + b^2).Apply Sum of Cubes Formula: Apply the sum of cubes formula to factor the expression. Using the formula, we have: 1 + r^9 = 1^3 + (r^3)^3 = (1 + r^3)(1^2 - 1*r^3 + r^6).Simplify Factored Expression: Simplify the factored expression. Simplifying the second factor, we get: (1 + r^3)(1 - r^3 + r^6).Check Further Factoring: Check for further factoring possibilities. The second factor (1 - r^3 + r^6) does not factor further using standard algebraic identities or methods for polynomials. Therefore, the expression is fully factored.

Factor completely: $\newline$ $1+r^{9}$ $\newline$ Answer:

Full solution

More problems from Factor quadratics: special cases

Related topics

Factor completely:\newline1+r9 1+r^{9} 1+r9\newlineAnswer:

Factor completely: $\newline$ $1+r^{9}$ $\newline$ Answer: