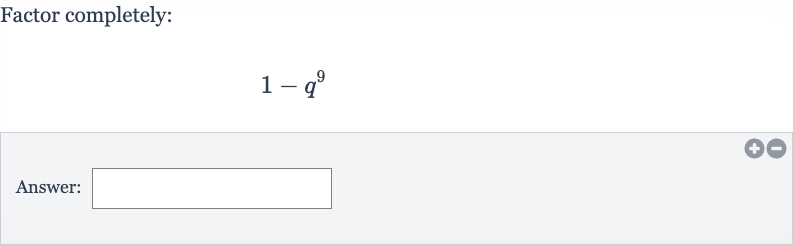
Factor completely: 1-q^(9) Answer:

Question

Factor completely:  1-q^(9) Answer:

Bytelearn · Accepted Answer

Identify type of factoring: Identify the type of factoring needed for 1 - q^9. The expression is a difference of two squares, where one term is 1 (which is 1^2) and the other is q^9. Since q^9 is a perfect square (q^3)^2, we can apply the difference of squares formula: a^2 - b^2 = (a - b)(a + b).Apply difference of squares: Apply the difference of squares formula to 1 - q^9. We have 1^2 - (q^3)^2, which can be factored as (1 - q^3)(1 + q^3).Recognize difference of cubes: Recognize that 1 + q^3 is not factorable over the real numbers, but 1 - q^3 is a difference of cubes. The difference of cubes formula is a^3 - b^3 = (a - b)(a^2 + ab + b^2). We can apply this to 1 - q^3.Apply difference of cubes: Apply the difference of cubes formula to 1 - q^3. We have 1^3 - q^3, which can be factored as (1 - q)(1^2 + 1*q + q^2), which simplifies to (1 - q)(1 + q + q^2).Combine factored forms: Combine the factored forms from Step 2 and Step 4. The completely factored form of 1 - q^9 is (1 - q)(1 + q + q^2)(1 + q^3).

Factor completely: $\newline$ $1-q^{9}$ $\newline$ Answer:

Full solution

More problems from Factor quadratics: special cases

Related topics

Factor completely:\newline1−q9 1-q^{9} 1−q9\newlineAnswer:

Factor completely: $\newline$ $1-q^{9}$ $\newline$ Answer: