AI tutor
Full solution
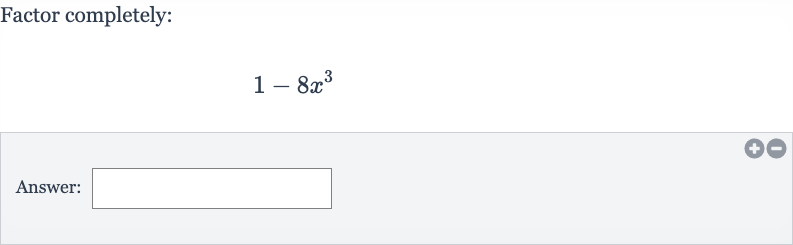
Q. Factor completely:Answer:
- Recognize Cubic Expression: Recognize the expression as a difference of cubes.A difference of cubes can be factored using the formula .Here, can be written as and can be written as .
- Apply Difference of Cubes Formula: Apply the difference of cubes formula.Let and .The factored form will be .
- Simplify Factored Form: Simplify the factored form.Simplify the second term to .The fully factored form is .