AI tutor
Full solution
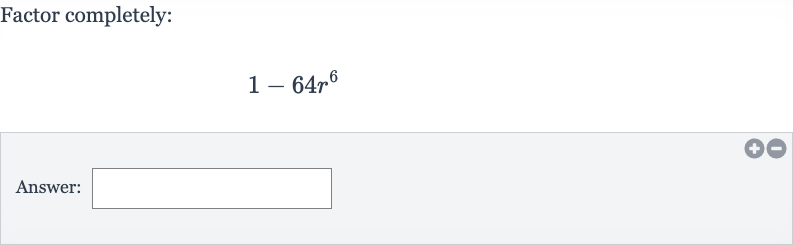
Q. Factor completely:Answer:
- Question Prompt: Question prompt: What is the factored form of the expression ?
- Recognize as Difference of Squares: Recognize the expression as a difference of squares.The expression can be written as , which is a difference of two squares.
- Apply Formula: Apply the difference of squares formula.The difference of squares formula is . Here, and .
- Factor Using Formula: Factor the expression using the formula.Substitute and into the formula to get .
- Check Factored Expression: Check the factored expression. when multiplied out should give the original expression . Let's check:, which matches the original expression.