AI tutor
Full solution
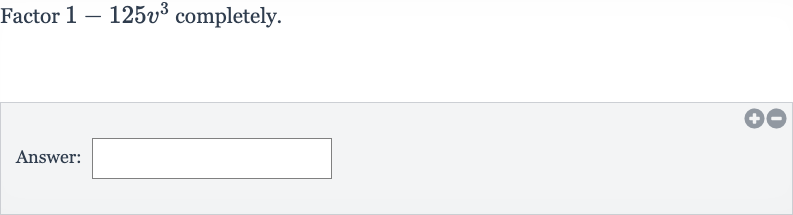
Q. Factor completely.Answer:
- Recognize Type of Expression: Recognize the type of expression we are dealing with.The expression can be seen as a difference of cubes since is and is .
- Apply Cubes Formula: Apply the difference of cubes formula.The difference of cubes formula is . Here, and .
- Substitute Values: Substitute the values of and into the formula.Using and , we get .
- Simplify Expression: Simplify the expression.Simplify the second factor: .So, the factored form is .