AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
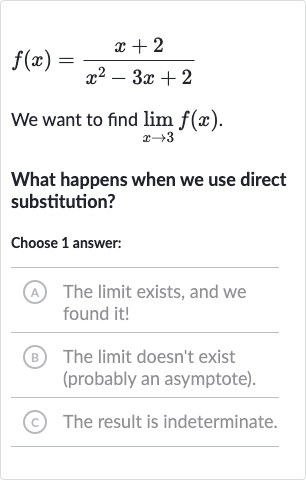
We want to find .What happens when we use direct substitution?Choose answer:(A) The limit exists, and we found it!(B) The limit doesn't exist (probably an asymptote).(C) The result is indeterminate.
Full solution
Q. We want to find .What happens when we use direct substitution?Choose answer:(A) The limit exists, and we found it!(B) The limit doesn't exist (probably an asymptote).(C) The result is indeterminate.
- Direct Substitution: Let's first try direct substitution by plugging into the function to see what we get.
- Performing Calculations: Now, let's perform the calculations:
- Simplifying the Expression: Simplify the expression:
- Existence of the Limit: Since we were able to find a value by direct substitution without encountering division by or any other undefined operations, the limit exists and we have found it.
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
