AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
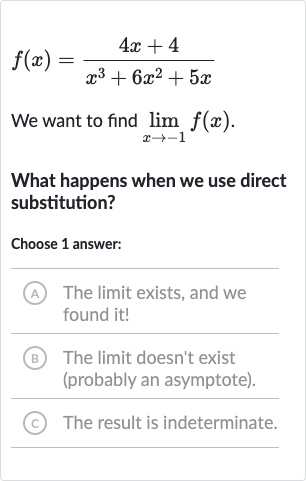
We want to find .What happens when we use direct substitution?Choose answer:(A) The limit exists, and we found it!(B) The limit doesn't exist (probably an asymptote).(C) The result is indeterminate.
Full solution
Q. We want to find .What happens when we use direct substitution?Choose answer:(A) The limit exists, and we found it!(B) The limit doesn't exist (probably an asymptote).(C) The result is indeterminate.
- Direct Substitution: Let's first try direct substitution by plugging into the function to see what we get.
- Perform Calculations: Now, let's perform the calculations:
- Simplify Numerator and Denominator: Simplify the numerator and the denominator: We get an indeterminate form , which means direct substitution does not give us the limit.
- Indeterminate Form: Since we have an indeterminate form, we cannot conclude the limit exists or doesn't exist based on direct substitution alone. We need to do further analysis or simplification to find the limit.
More problems from Power rule
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
