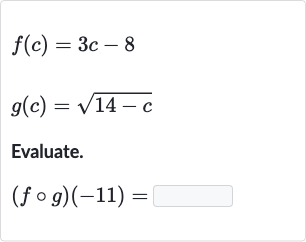AI tutor
Full solution
Q. Evaluate.
- Understand Function Composition: Understand the composition of functions. The composition of functions means that we first apply to , and then apply to the result of . So, .
- Evaluate : Evaluate . We need to find the value of when . So, we calculate .
- Simplify : Simplify . The square root of is , so .
- Evaluate : Evaluate . Now we need to apply to the result of , which is . So, we calculate .
- Simplify : Simplify .Multiplying by gives us , and subtracting from gives us . So, .
More problems from Domain and range of square root functions: equations
QuestionGet tutor help
QuestionGet tutor help