Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Express the given expression without logs, in simplest form. Assume all variables represent positive values.

(8^(log_(8)(6w^(3))+log_(8)(2z^(3))))
Answer:

Express the given expression without logs, in simplest form. Assume all variables represent positive values. $\newline$ $\left(8^{\log _{8}\left(6 w^{3}\right)+\log _{8}\left(2 z^{3}\right)}\right)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

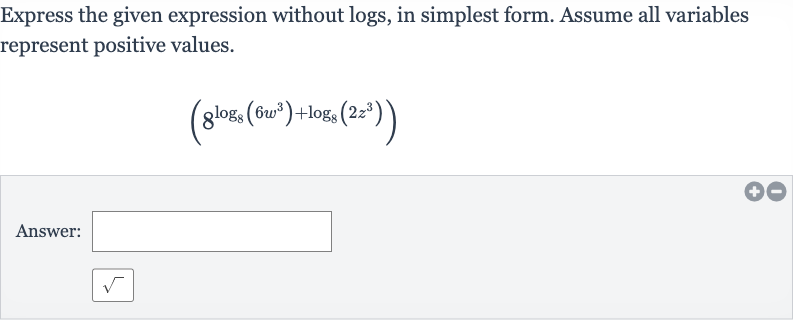
Q. Express the given expression without logs, in simplest form. Assume all variables represent positive values.

\newline

\left(8^{\log _{8}\left(6 w^{3}\right)+\log _{8}\left(2 z^{3}\right)}\right)

\newline

Answer:

Apply Logarithm Properties: Apply the properties of logarithms to combine the log terms. $\newline$ The expression given is $8^{\log_{8}(6w^{3}) + \log_{8}(2z^{3})}$ . According to the properties of logarithms, specifically the product rule, $\log_b(m) + \log_b(n) = \log_b(m*n)$ , we can combine the log terms under a single log with base $8$ .
Combine Log Terms: Combine the log terms using the product rule. $\newline$ Using the product rule, we get: $\newline$ $8^{\log_{8}(6w^{3} \cdot 2z^{3})}$
Simplify Inside Log: Simplify the expression inside the log. $\newline$ Now we multiply the terms inside the log: $\newline$ $6w^{3} \times 2z^{3} = 12w^{3}z^{3}$ $\newline$ So the expression becomes: $\newline$ $8^{\log_{8}(12w^{3}z^{3})}$
Apply Property of Logarithms: Apply the property of logarithms that $b^{\log_b(x)} = x$ . According to this property, since the base of the log and the base of the exponent are the same, the expression simplifies to the argument of the log: $8^{\log_{8}(12w^{3}z^{3})} = 12w^{3}z^{3}$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant