Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Express the given expression without logs, in simplest form. Assume all variables represent positive values.

(4^(log_(4)(5sqrty)))
Answer:

Express the given expression without logs, in simplest form. Assume all variables represent positive values. $\newline$ $\left(4^{\log _{4}(5 \sqrt{y})}\right)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Full solution

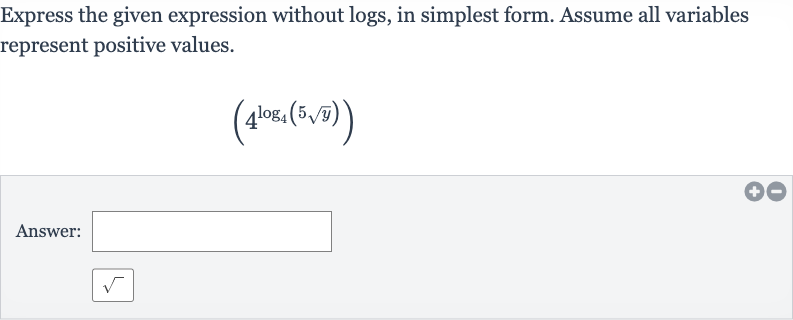
Q. Express the given expression without logs, in simplest form. Assume all variables represent positive values.

\newline

\left(4^{\log _{4}(5 \sqrt{y})}\right)

\newline

Answer:

Apply Property: We are given the expression $4^{\log_{4}(5\sqrt{y})}$ . To express this without logs, we use the property that $a^{\log_a(b)} = b$ , where $a$ is the base of the logarithm and $b$ is the argument of the logarithm.
Simplify Expression: Applying the property to our expression, we have: $\newline$ $4^{\log_{4}(5\sqrt{y})} = 5\sqrt{y}$ $\newline$ This is because the base of the logarithm ( $4$ ) and the base of the exponent ( $4$ ) are the same.
Final Result: Now, we simplify the expression $5\sqrt{y}$ . Since there are no further logarithms or exponents to simplify, this is already in its simplest form.

More problems from Power rule

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant