Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Express the given expression without logs, in simplest form. Assume all variables represent positive values.

(3^(-3log_(3)4x^(2)))
Answer:

Express the given expression without logs, in simplest form. Assume all variables represent positive values. $\newline$ $\left(3^{-3 \log _{3} 4 x^{2}}\right)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

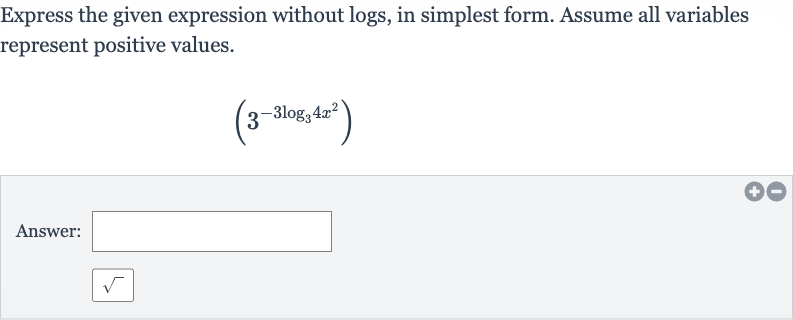
Q. Express the given expression without logs, in simplest form. Assume all variables represent positive values.

\newline

\left(3^{-3 \log _{3} 4 x^{2}}\right)

\newline

Answer:

Understand and Apply Power Rule: Understand the given expression and apply the power rule of logarithms. $\newline$ The expression is $3^{-3\log_{3}4x^{2}}$ . According to the power rule of logarithms, $a^{\log_{a}(b)} = b$ . We will use this rule to simplify the expression.
Apply Power Rule to Logarithmic Part: Apply the power rule to the logarithmic part of the expression. $\newline$ The power rule states that $a^{(n\log_a(b))} = b^n$ . Here, $a = 3$ , $n = -3$ , and $\log_a(b) = \log_{3}4x^{2}$ . So we can rewrite the expression as $(4x^{2})^{-3}$ .
Simplify Using Power of a Power Rule: Simplify the expression using the power of a power rule. $\newline$ The power of a power rule states that $(b^n)^m = b^{n*m}$ . Applying this rule, we get $4^{-3} \times (x^{2})^{-3}$ .
Calculate Powers to Simplify: Simplify the expression further by calculating the powers. $4^{-3} = \frac{1}{4^3} = \frac{1}{64}$ and $(x^{2})^{-3} = \frac{1}{(x^{2*3})} = \frac{1}{x^6}$ . So the expression becomes $\frac{1}{64} * \frac{1}{x^6}.$
Combine Fractions for Final Expression: Combine the fractions to get the final simplified expression. $\newline$ Multiplying the fractions, we get $\frac{1}{64x^6}$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant