Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

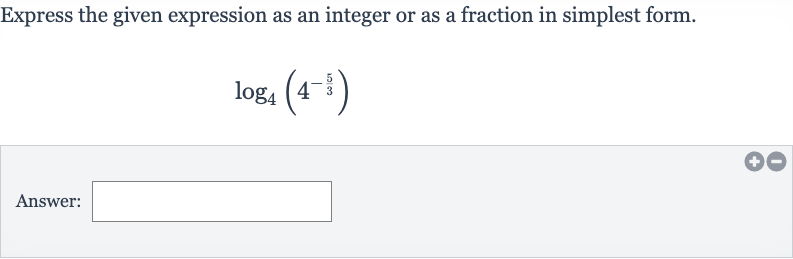
$Express the given expression as an integer or as a fraction in simplest form. log_(4)(4^(-(5)/(3))) Answer:$

Express the given expression as an integer or as a fraction in simplest form. $\newline$ $\log _{4}\left(4^{-\frac{5}{3}}\right)$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the given expression as an integer or as a fraction in simplest form.

\newline

\log _{4}\left(4^{-\frac{5}{3}}\right)

\newline

Answer:

Understand Logarithm Properties: Understand the properties of logarithms. The logarithm of a power of the base simplifies to the exponent times the logarithm of the base to the base itself. In this case, we have $\log_{4}(4^{x})$ . The property we use is $\log_{b}(b^{x}) = x$ , where $b$ is the base of the logarithm and $x$ is the exponent.
Apply Logarithm Power Rule: Apply the logarithm power rule. $\newline$ Using the property from Step $1$ , we can simplify $\log_{4}(4^{-\frac{5}{3}})$ to just the exponent, which is $-\frac{5}{3}$ , because the base of the logarithm and the base of the power are the same (both are $4$ ). $\newline$ $\log_{4}(4^{-\frac{5}{3}}) = -\frac{5}{3}$
Express Result as Fraction: Express the result as an integer or a fraction. $\newline$ The result from Step $2$ is already in the form of a fraction, which is the simplest form for this expression. There is no need to convert it to an integer because $-\frac{5}{3}$ cannot be expressed as an integer.

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant