Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

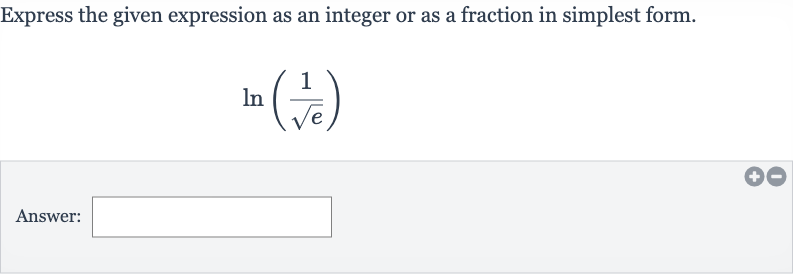
Express the given expression as an integer or as a fraction in simplest form. ln((1)/(sqrte)) Answer:

Express the given expression as an integer or as a fraction in simplest form.\newlineln⁡(1e) \ln \left(\frac{1}{\sqrt{e}}\right) \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Roots of rational numbersright chevron icon

Full solution

Q. Express the given expression as an integer or as a fraction in simplest form.\newlineln⁡(1e) \ln \left(\frac{1}{\sqrt{e}}\right) \newlineAnswer:
  1. Understand the expression: Understand the given expression.\newlineWe need to simplify the natural logarithm of the reciprocal of the square root of ee, which is ln⁡(1e)\ln\left(\frac{1}{\sqrt{e}}\right).
  2. Apply logarithm properties: Apply the properties of logarithms.\newlineThe natural logarithm of a reciprocal is the negative of the natural logarithm of the original value. Also, the natural logarithm of the square root of a number is one-half the natural logarithm of the number itself.\newlineln⁡(1e)=−ln⁡(e)=−12×ln⁡(e)\ln\left(\frac{1}{\sqrt{e}}\right) = -\ln(\sqrt{e}) = -\frac{1}{2} \times \ln(e)
  3. Simplify ln⁡(e)\ln(e): Simplify the natural logarithm of ee.\newlineSince the natural logarithm of ee is 11 (ln⁡(e)=1\ln(e) = 1), we can simplify the expression further.\newline−12×ln⁡(e)=−12×1=−12-\frac{1}{2} \times \ln(e) = -\frac{1}{2} \times 1 = -\frac{1}{2}

More problems from Roots of rational numbers

Question
Find the real-number root. \newline16\sqrt{16}\newline\newlineWrite your answer in simplified form. \newline____\_\_\_\_
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the real-number root. \newline916\sqrt{\frac{9}{16}}\newlineSimplify your answer and write it as a decimal or as a proper or improper fraction.\newline_____\_\_\_\_\_
Get tutor helpright-arrow

Posted 9 months ago

Question
Find the real-number root using a calculator. Round your answer to the nearest thousandth. \newline`\sqrt{957} `\newline _______
Get tutor helpright-arrow

Posted 9 months ago

Question
Multiply. Write your answer in simplest form. \newline273×42\sqrt{273} \times \sqrt{42}\newline______
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. \newline634\sqrt{\frac{63}{4}}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Rationalize the denominator.\newline−49−2\frac{-4}{9 - \sqrt{2}}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve for z z .\newline16=z 16 = \sqrt{z} \newlinez= z = _____
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify the radical expression. 14x14 \sqrt{14x^{14}} Write your answer in the form A A , B \sqrt{B} , or AB A\sqrt{B} , where A A and B B are constants or expressions in x x . Use at most one radical in your answer, and at most one absolute value symbol in your expression for A A . ______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify the radical expression.\newline12x12\sqrt{12x^{12}}\newlineWrite your answer in the form AA, B\sqrt{B}, or ABA\sqrt{B}, where AA and BB are constants or expressions in xx. Use at most one radical in your answer, and at most one absolute value symbol in your expression for AA.\newline‾\underline{\hspace{3cm}}
Get tutor helpright-arrow

Posted 9 months ago

Question
What is the value of sin⁡(5π6)? \sin \left(\frac{5 \pi}{6}\right) ? \newlineChoose 11 answer:\newline(A) −32 -\frac{\sqrt{3}}{2} \newline(B) −22 -\frac{\sqrt{2}}{2} \newline(C) 12 \frac{1}{2} \newline(D) 150150
Get tutor helpright-arrow

Posted 10 months ago

View all (169)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant