Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

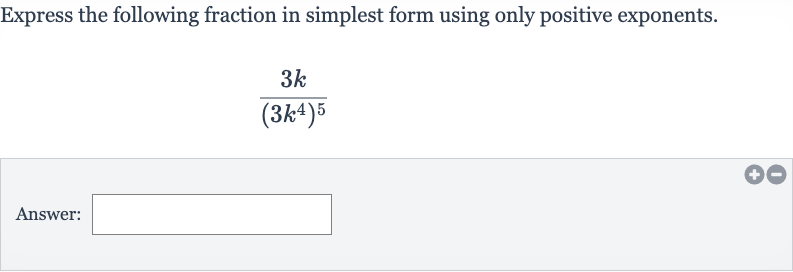
$Express the following fraction in simplest form using only positive exponents. (3k)/((3k^(4))^(5)) Answer:$

Express the following fraction in simplest form using only positive exponents. $\newline$ $\frac{3 k}{\left(3 k^{4}\right)^{5}}$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 1

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form using only positive exponents.

\newline

\frac{3 k}{\left(3 k^{4}\right)^{5}}

\newline

Answer:

Write & Apply Power Rule: Write down the given expression and apply the power of a power rule. $\newline$ The power of a power rule states that $(a^{m})^{n} = a^{m*n}$ . We will apply this rule to the denominator of the given fraction. $\newline$ $\frac{3k}{(3k^{4})^{5}}$
Simplify Denominator: Apply the power of a power rule to the denominator. $\newline$ $(3k^{4})^{5} = 3^{5} \times k^{4\times5} = 3^{5} \times k^{20}$ $\newline$ Now, rewrite the original expression with the simplified denominator. $\newline$ $\frac{3k}{3^{5} \times k^{20}}$
Divide Common Terms: Simplify the fraction by dividing both the numerator and the denominator by the common terms. $\newline$ The term $3k$ in the numerator can be divided by $3$ , and $k$ can be divided by $k^{20}$ . $\newline$ $\frac{3k}{3^5 \cdot k^{20}} = \frac{3}{3^5} \cdot \frac{k}{k^{20}}$
Further Simplify Terms: Simplify the terms further. $\newline$ $(\frac{3}{3^5}) = 3^{(1-5)} = 3^{-4}$ $\newline$ $(\frac{k}{k^{20}}) = k^{(1-20)} = k^{-19}$ $\newline$ Now, combine the simplified terms. $\newline$ $3^{-4} \cdot k^{-19}$
Reciprocal of Negative Exponents: Since we need to express the answer with only positive exponents, we will take the reciprocal of the terms with negative exponents. $\newline$ $3^{-4} = \frac{1}{3^4}$ $\newline$ $k^{-19} = \frac{1}{k^{19}}$ $\newline$ Now, write the expression with positive exponents. $\newline$ $\frac{1}{3^4 \cdot k^{19}}$
Final Simplified Expression: Write the final simplified expression. $\newline$ The final simplified form of the given fraction is: $\newline$ $\frac{1}{3^4 \cdot k^{19}}$