Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

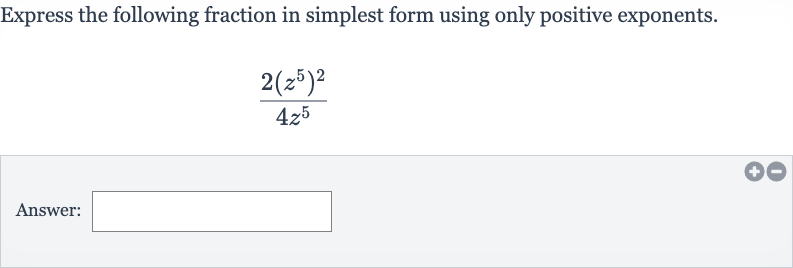
$Express the following fraction in simplest form using only positive exponents. (2(z^(5))^(2))/(4z^(5)) Answer:$

Express the following fraction in simplest form using only positive exponents. $\newline$ $\frac{2\left(z^{5}\right)^{2}}{4 z^{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form using only positive exponents.

\newline

\frac{2\left(z^{5}\right)^{2}}{4 z^{5}}

\newline

Answer:

Apply Power Rule: Simplify the numerator by applying the power of a power rule. $\newline$ The power of a power rule states that $(a^m)^n = a^{m*n}$ . Therefore, we can simplify the numerator as follows: $\newline$ $(2(z^{5})^{2}) = 2 \times (z^{5*2}) = 2 \times z^{10}$
Divide Numerator and Denominator: Simplify the fraction by dividing the numerator by the denominator. $\newline$ We have the fraction $(2 \cdot z^{10}) / (4z^{5})$ . To simplify, we divide both the coefficients and the like terms with exponents. $\newline$ $(2 \cdot z^{10}) / (4z^{5}) = (2/4) \cdot (z^{10-5})$
Simplify Coefficients and Exponents: Simplify the coefficients and subtract the exponents. $\newline$ Simplifying the coefficients $\frac{2}{4}$ gives us $\frac{1}{2}$ . Subtracting the exponents gives us $z^{(10-5)} = z^5$ . $\newline$ So, $(\frac{\(2\)}{\(4\)}) \cdot (z^{(\(10\)\(-5\))}) = (\frac{\(1\)}{\(2\)}) \cdot z^\(5\)
Write Final Expression: Write the final simplified expression.\(\newline\)The final simplified expression is \((\frac{1}{2}) \times z^5\), which can also be written as \(\frac{z^5}{2}\).

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant