Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

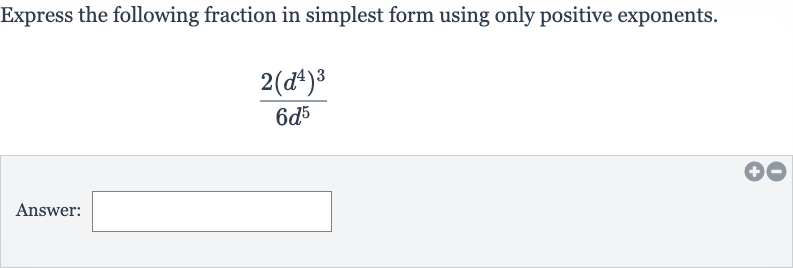
$Express the following fraction in simplest form using only positive exponents. (2(d^(4))^(3))/(6d^(5)) Answer:$

Express the following fraction in simplest form using only positive exponents. $\newline$ $\frac{2\left(d^{4}\right)^{3}}{6 d^{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form using only positive exponents.

\newline

\frac{2\left(d^{4}\right)^{3}}{6 d^{5}}

\newline

Answer:

Simplify numerator: Simplify the numerator. $\newline$ The numerator is $2(d^{4})^{3}$ . According to the power of a power rule, $(a^{m})^{n} = a^{m*n}$ , we multiply the exponents. $\newline$ $2(d^{4*3})$ $\newline$ = $2(d^{12})$
Simplify denominator: Simplify the denominator. $\newline$ The denominator is $6d^{5}$ . There is nothing to simplify here, so we keep it as is. $\newline$ $6d^{5}$
Divide numerator by denominator: Divide the numerator by the denominator. $\newline$ Now we divide the terms in the numerator by the corresponding terms in the denominator. $\newline$ $(2d^{12})/(6d^{5})$ $\newline$ We can divide the coefficients $(2/6)$ and subtract the exponents of $d$ $(d^{12-5})$ since the bases are the same. $\newline$ $(1/3)d^{12-5}$ $\newline$ = $(1/3)d^{7}$
Check for further simplification: Check for any further simplification. $\newline$ The fraction $(\frac{1}{3})d^{7}$ is already in its simplest form with positive exponents. There are no common factors to cancel out, and the exponent is already positive.

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant