Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

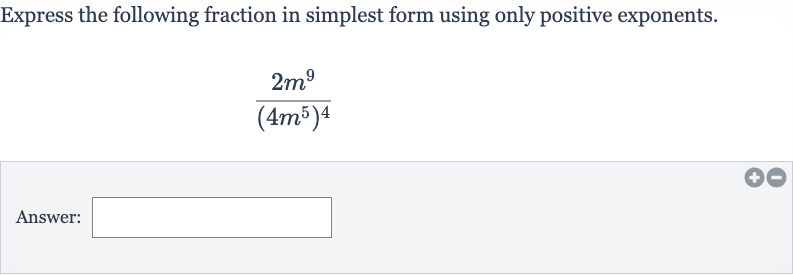
$Express the following fraction in simplest form using only positive exponents. (2m^(9))/((4m^(5))^(4)) Answer:$

Express the following fraction in simplest form using only positive exponents. $\newline$ $\frac{2 m^{9}}{\left(4 m^{5}\right)^{4}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form using only positive exponents.

\newline

\frac{2 m^{9}}{\left(4 m^{5}\right)^{4}}

\newline

Answer:

Write Expression: Write down the given expression. $\newline$ We have the expression $(2m^{9})/((4m^{5})^{4})$ .
Simplify Denominator: Simplify the denominator. $\newline$ The denominator $(4m^{5})^{4}$ can be simplified by raising both the base $4$ and the term $m^{5}$ to the power of $4$ . $\newline$ $(4m^{5})^{4} = 4^{4} \times (m^{5})^{4}$ $\newline$ $= 256 \times m^{20}$ since $4^4 = 256$ and $(m^{5})^4 = m^{5\times4} = m^{20}$ .
Rewrite with Simplified Denominator: Rewrite the expression with the simplified denominator. $\newline$ Now the expression becomes: $\newline$ $(2m^{9}) / (256m^{20})$
Simplify Fraction: Simplify the fraction by dividing the coefficients and subtracting the exponents. $\newline$ Divide the coefficients: $\frac{2}{256} = \frac{1}{128}$ $\newline$ Subtract the exponents of $m$ : $m^{9-20} = m^{-11}$ $\newline$ The expression now is $\frac{1}{128} \times m^{-11}.$
Express Negative Exponent: Express the negative exponent as a positive exponent. $\newline$ Since we want only positive exponents, we can write $m^{-11}$ as $1/m^{11}$ . $\newline$ The expression now is $(1/128) \times (1/m^{11})$ .
Combine Fractions: Combine the fractions. $\newline$ The expression $(\frac{1}{128}) \times (\frac{1}{m^{11}})$ can be combined into a single fraction: $\newline$ $\frac{1}{128m^{11}}$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant