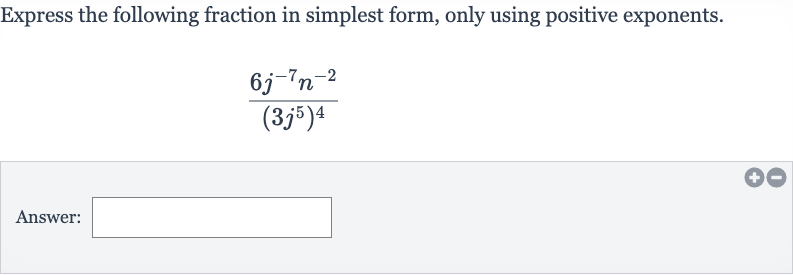
Express the following fraction in simplest form, only using positive exponents. (6j^(-7)n^(-2))/((3j^(5))^(4)) Answer:

Question

Express the following fraction in simplest form, only using positive exponents.  (6j^(-7)n^(-2))/((3j^(5))^(4)) Answer:

Bytelearn · Accepted Answer

Write Expression and Identify Negative Exponents: Write down the given expression and identify the negative exponents. The given expression is (6j^(-7)n^(-2))/((3j^(5))^(4)). We need to simplify this expression and express it with only positive exponents.Apply Power Rule to Denominator: Apply the power rule to the denominator. The power rule states that (a^m)^n = a^(m*n). We apply this to the denominator (3j^(5))^(4). (3j^(5))^(4) = 3^4 * (j^5)^4 = 81 * j^(5*4) = 81 * j^20.Rewrite Expression with Positive Exponents: Rewrite the expression with positive exponents by moving the terms with negative exponents from the numerator to the denominator and vice versa. 6j^(-7)n^(-2) can be rewritten as 6/(j^7n^2). Now the expression is 6/(j^7n^2) divided by 81 * j^20.Divide Numerators and Denominators: Divide the numerators and the denominators separately. To divide fractions, we multiply the first fraction by the reciprocal of the second fraction. So, (6/(j^7n^2)) / (81 * j^20) becomes (6/(j^7n^2)) * (1/(81 * j^20)).Multiply Numerators and Denominators: Multiply the numerators and the denominators. Multiplying the numerators: 6 * 1 = 6. Multiplying the denominators: (j^7n^2) * (81 * j^20) = 81 * j^(7+20) * n^2 = 81 * j^27 * n^2. Now the expression is 6/(81 * j^27 * n^2).Simplify Fraction by Reducing Common Factors: Simplify the fraction by reducing common factors. The number 6 is a factor of 81, so we can simplify the fraction by dividing both the numerator and the denominator by 6. 6/81 simplifies to 1/13.5 (since 6/81 = 1/13.5). Now the expression is 1/(13.5 * j^27 * n^2).

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{6 j^{-7} n^{-2}}{\left(3 j^{5}\right)^{4}}$ $\newline$ Answer:

Full solution

More problems from Multiplication with rational exponents

Related topics

Express the following fraction in simplest form, only using positive exponents.\newline6j−7n−2(3j5)4 \frac{6 j^{-7} n^{-2}}{\left(3 j^{5}\right)^{4}} (3j5)46j−7n−2​\newlineAnswer:

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{6 j^{-7} n^{-2}}{\left(3 j^{5}\right)^{4}}$ $\newline$ Answer: