Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

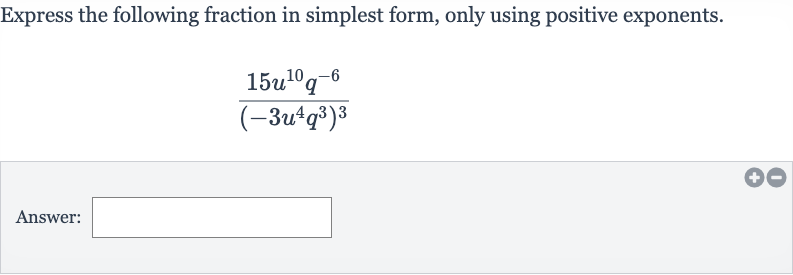
$Express the following fraction in simplest form, only using positive exponents. (15u^(10)q^(-6))/((-3u^(4)q^(3))^(3)) Answer:$

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{15 u^{10} q^{-6}}{\left(-3 u^{4} q^{3}\right)^{3}}$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 1

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form, only using positive exponents.

\newline

\frac{15 u^{10} q^{-6}}{\left(-3 u^{4} q^{3}\right)^{3}}

\newline

Answer:

Simplify Denominator: Simplify the denominator. $\newline$ We have a negative base raised to an exponent: $(-3u^{4}q^{3})^{3}$ . When raising a negative base to an odd exponent, the result is negative. We will also distribute the exponent of $3$ to each factor inside the parentheses. $\newline$ $(-3u^{4}q^{3})^{3} = -3^{3} \times u^{4\times3} \times q^{3\times3}$ $\newline$ $= -27 \times u^{12} \times q^{9}$
Rewrite Fraction: Rewrite the original fraction with the simplified denominator. $\newline$ Now we have the fraction as: $\newline$ $(\frac{15u^{10}q^{-6}}{-27u^{12}q^{9}})$
Simplify Fraction: Simplify the fraction by dividing the coefficients and subtracting the exponents of like bases. $\newline$ We divide the coefficients $15$ and $-27$ and subtract the exponents of $u$ and $q$ . $\newline$ For the coefficients: $\frac{15}{-27} = -\frac{5}{9}$ $\newline$ For $u$ : $u^{10} / u^{12} = u^{10-12} = u^{-2}$ $\newline$ For $q$ : $q^{-6} / q^{9} = q^{-6-9} = q^{-15}$ $\newline$ The fraction simplifies to: $\newline$ $(-\frac{5}{9}) \cdot u^{-2} \cdot q^{-15}$
Express with Positive Exponents: Express the fraction using only positive exponents. $\newline$ To express $u^{-2}$ and $q^{-15}$ with positive exponents, we take the reciprocal of each. $\newline$ $u^{-2} = \frac{1}{u^{2}}$ $\newline$ $q^{-15} = \frac{1}{q^{15}}$ $\newline$ The fraction becomes: $\newline$ $\left(-\frac{5}{9}\right) \cdot \left(\frac{1}{u^{2}}\right) \cdot \left(\frac{1}{q^{15}}\right)$
Combine Terms: Combine the terms to get the final answer. $\newline$ The final simplified form of the fraction is: $\newline$ $-\frac{5}{9u^{2}q^{15}}$