Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

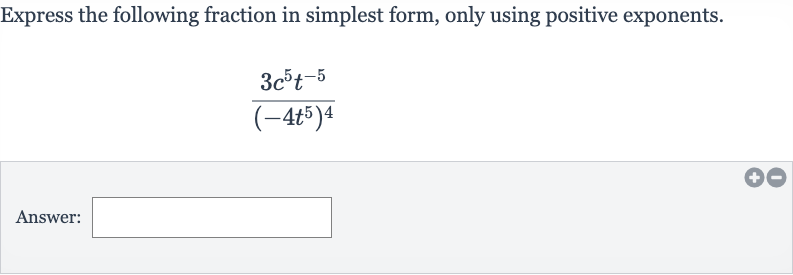
$Express the following fraction in simplest form, only using positive exponents. (3c^(5)t^(-5))/((-4t^(5))^(4)) Answer:$

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{3 c^{5} t^{-5}}{\left(-4 t^{5}\right)^{4}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form, only using positive exponents.

\newline

\frac{3 c^{5} t^{-5}}{\left(-4 t^{5}\right)^{4}}

\newline

Answer:

Identify Given Expression: Write down the given expression and identify negative exponents. $\newline$ The given expression is $(3c^{5}t^{-5})/((-4t^{5})^{4})$ . $\newline$ We can see that $t^{-5}$ is a negative exponent.
Apply Negative Exponent Rule: Apply the negative exponent rule to move $t^{-5}$ to the denominator. $\newline$ According to the negative exponent rule, $a^{-n} = \frac{1}{a^n}$ . We apply this to $t^{-5}$ . $\newline$ $(3c^{5}t^{-5})/((-4t^{5})^{4})$ becomes $(3c^{5})/(t^{5}(-4t^{5})^4)$ .
Simplify Denominator: Simplify the denominator. $\newline$ We need to simplify $(-4t^{5})^4$ . When raising a power to a power, we multiply the exponents, and when raising a product to a power, we raise each factor to the power. $\newline$ $(-4t^{5})^4 = (-4)^4 \times (t^{5})^4 = 256 \times t^{20}$ .
Substitute Simplified Denominator: Substitute the simplified denominator back into the expression. $\newline$ Now we have $(3c^{5})/(t^{5} \cdot 256 \cdot t^{20})$ .
Combine T Terms: Combine the $t$ terms in the denominator. $\newline$ Since $t^{5} \times t^{20} = t^{5+20} = t^{25}$ , we can combine them. $\newline$ The expression now is $(3c^{5})/(256 \times t^{25})$ .
Simplify Fraction: Simplify the fraction by canceling out any common factors if possible. $\newline$ There are no common factors between the numerator and the denominator, so the expression is already in its simplest form. $\newline$ The final answer is $(3c^{5})/(256 \times t^{25})$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant