Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

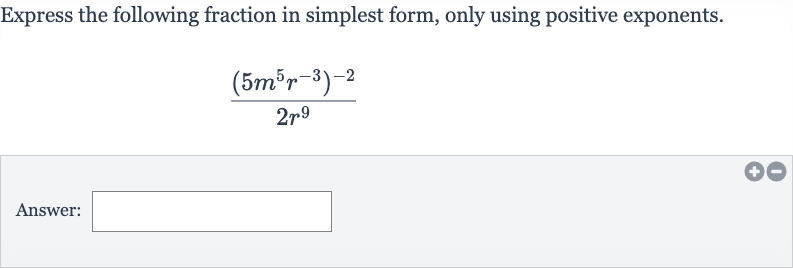
$Express the following fraction in simplest form, only using positive exponents. ((5m^(5)r^(-3))^(-2))/(2r^(9)) Answer:$

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{\left(5 m^{5} r^{-3}\right)^{-2}}{2 r^{9}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form, only using positive exponents.

\newline

\frac{\left(5 m^{5} r^{-3}\right)^{-2}}{2 r^{9}}

\newline

Answer:

Apply Negative Exponent Rule: Write down the given expression and apply the negative exponent rule. $\newline$ The negative exponent rule states that $a^{-n} = \frac{1}{a^n}$ . We will apply this rule to simplify the expression. $\newline$ Given expression: $\left(\left(5m^{5}r^{-3}\right)^{-2}\right)/\left(2r^{9}\right)$ $\newline$ Apply the negative exponent rule to the numerator: $\newline$ $= \left(\frac{1}{\left(5m^{5}r^{-3}\right)^{2}}\right)/\left(2r^{9}\right)$
Simplify Numerator with Power of a Power Rule: Simplify the numerator by applying the power of a power rule. $\newline$ The power of a power rule states that $(a^n)^m = a^{n*m}$ . We will apply this rule to the numerator. $\newline$ $= \frac{1}{((5^2)(m^{5*2})(r^{-3*2}))}/(2r^{9})$ $\newline$ $= \frac{1}{(25m^{10}r^{-6})}/(2r^{9})$
Simplify Denominator by Multiplying Exponents: Simplify the denominator by multiplying the exponents. $\newline$ Since we have a single term $r^{9}$ in the denominator, we can combine it with the numerator. $\newline$ = $\frac{1}{25m^{10}r^{-6} \times 2r^{9}}$ $\newline$ = $\frac{1}{50m^{10}r^{(-6+9)}}$ $\newline$ = $\frac{1}{50m^{10}r^{3}}$
Rewrite Expression with Positive Exponents: Rewrite the expression with only positive exponents. $\newline$ We already have only positive exponents in the expression, so no further simplification is needed in terms of exponents. $\newline$ Final expression: $\frac{1}{50m^{10}r^{3}}$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant