Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

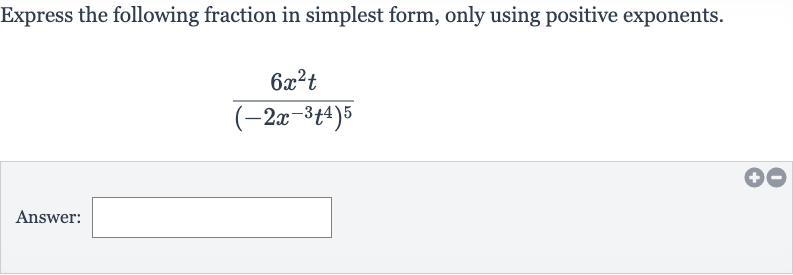
$Express the following fraction in simplest form, only using positive exponents. (6x^(2)t)/((-2x^(-3)t^(4))^(5)) Answer:$

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{6 x^{2} t}{\left(-2 x^{-3} t^{4}\right)^{5}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form, only using positive exponents.

\newline

\frac{6 x^{2} t}{\left(-2 x^{-3} t^{4}\right)^{5}}

\newline

Answer:

Distribute Exponent of $5$ : We need to simplify the fraction $\frac{6x^{2}t}{(-2x^{-3}t^{4})^{5}}$ . First, let's simplify the denominator by distributing the exponent of $5$ to each factor inside the parentheses.
Apply Power of Power Rule: Apply the power of a power rule: a*b)^n = a^n * b^n\. In this case, we have \$\left(-2x^{(-3)}t^{(4)}\right)^5 = (-2)^5 * \$x^{(-3)}^ $5$ * $t^{(4)}$ ^ $5$ \.
Calculate Parts Separately: Calculate each part separately: $(-2)^5 = -32$ , $(x^{-3})^5 = x^{-15}$ , and $(t^{4})^5 = t^{20}$ .
Rewrite Denominator: Now, rewrite the denominator with the calculated values: $(-2x^{-3}t^{4})^{5} = -32x^{-15}t^{20}$ .
Divide Numerator by Denominator: The fraction now looks like this: $(6x^{2}t)/(-32x^{-15}t^{20})$ . Next, we will divide the numerator by the denominator by subtracting the exponents of like bases and dividing the coefficients.
Divide Coefficients: Divide the coefficients: $\frac{6}{-32} = -\frac{3}{16}$ . Subtract the exponents of $x$ : $x^{(2 - (-15))} = x^{17}$ . Subtract the exponents of $t$ : $t^{(1 - 20)} = t^{-19}$ .
Subtract Exponents: Combine the results: $-\frac{3}{16} \times x^{17} \times t^{-19}$ . Since we want only positive exponents, we need to move $t^{-19}$ to the denominator.
Combine Results: The final simplified expression with positive exponents is: $(-3x^{17})/(16t^{19})$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant