Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

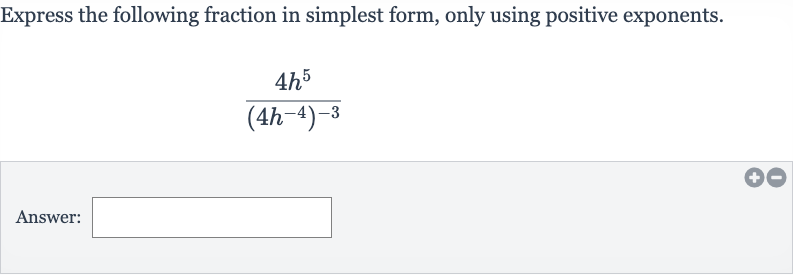
$Express the following fraction in simplest form, only using positive exponents. (4h^(5))/((4h^(-4))^(-3)) Answer:$

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{4 h^{5}}{\left(4 h^{-4}\right)^{-3}}$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 1

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form, only using positive exponents.

\newline

\frac{4 h^{5}}{\left(4 h^{-4}\right)^{-3}}

\newline

Answer:

Simplify Denominator: Simplify the denominator. $\newline$ We have a negative exponent in the denominator, which we can simplify by using the rule that $a^{-n} = \frac{1}{a^n}$ . $\newline$ $(4h^{-4})^{-3} = \left(\frac{1}{4h^4}\right)^{-3}$
Apply Negative Exponent: Apply the negative exponent to the denominator. $\newline$ Using the rule from Step $1$ , we can now apply the negative exponent to the denominator. $\newline$ $(1/(4h^4))^{-3} = (4h^4)^3$
Expand Exponent: Expand the exponent in the denominator. $\newline$ We will now expand the exponent in the denominator by multiplying the exponents. $\newline$ $(4h^4)^3 = 4^3 \times (h^4)^3$ $\newline$ $= 64 \times h^{4\times3}$ $\newline$ $= 64 \times h^{12}$
Combine Numerator and Denominator: Combine the numerator and the simplified denominator. $\newline$ Now we can combine the original numerator with the simplified denominator. $\newline$ $(4h^5) / (64 \cdot h^{12})$
Simplify Fraction: Simplify the fraction by dividing the coefficients and subtracting the exponents. $\newline$ We divide the coefficients $\frac{4}{64}$ and subtract the exponents of $h$ $(5 - 12)$ . $\newline$ $\frac{4}{64} \cdot h^{5-12}$ $\newline$ = $\frac{1}{16} \cdot h^{-7}$
Express Negative Exponent: Express the negative exponent as a positive exponent. $\newline$ We have a negative exponent in the result, which we can express as a positive exponent by taking the reciprocal. $\newline$ $(1/16) \times h^{-7} = (1/16) \times (1/h^7)$
Combine Terms: Combine the terms to express the final answer. $\newline$ The final answer is the product of the fraction and the reciprocal of $h$ to the positive exponent. $\newline$ $(\frac{1}{16}) \times (\frac{1}{h^7}) = \frac{1}{16h^7}$