Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

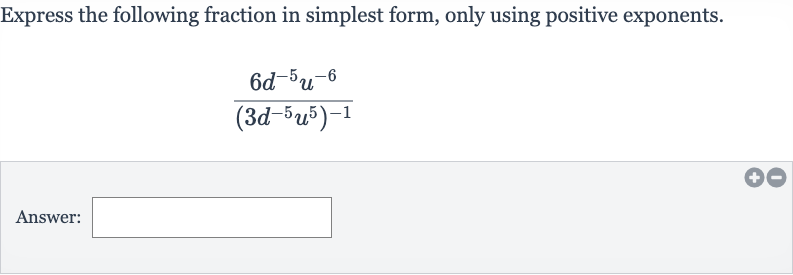
$Express the following fraction in simplest form, only using positive exponents. (6d^(-5)u^(-6))/((3d^(-5)u^(5))^(-1)) Answer:$

Express the following fraction in simplest form, only using positive exponents. $\newline$ $\frac{6 d^{-5} u^{-6}}{\left(3 d^{-5} u^{5}\right)^{-1}}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Express the following fraction in simplest form, only using positive exponents.

\newline

\frac{6 d^{-5} u^{-6}}{\left(3 d^{-5} u^{5}\right)^{-1}}

\newline

Answer:

Invert denominator: We start by simplifying the denominator which is raised to the power of $-1$ . Raising a fraction to the power of $-1$ inverts the fraction. $\newline$ $(3d^{-5}u^{5})^{-1} = \frac{1}{3d^{-5}u^{5}}$
Multiply numerator and denominator: Now we simplify the expression by multiplying the numerator by the inverted denominator. $\newline$ $(6d^{-5}u^{-6}) \times (1/(3d^{-5}u^{5}))$
Cancel common terms: We can simplify the expression by canceling out the common terms in the numerator and the denominator. The $d^{-5}$ terms cancel each other out. $\newline$ $(6u^{-6}) \cdot \left(\frac{1}{3u^{5}}\right)$
Simplify remaining terms: Now we multiply the remaining terms. The $6$ in the numerator and the $3$ in the denominator can be simplified to $2$ (since $6/3 = 2$ ). $\newline$ $2u^{-6} \times u^{5}$
Combine $u$ terms: We combine the $u$ terms by subtracting the exponents, since they are being divided. $2u^{(-6 + 5)}$
Subtract exponents: We perform the subtraction of the exponents. $2u^{-1}$
Rewrite $u^{-1}$ : To express the fraction with only positive exponents, we rewrite $u^{-1}$ as $\frac{1}{u}$ . $\newline$ $2 \times \left(\frac{1}{u}\right)$
Express as single fraction: Finally, we write the expression as a single fraction. $\frac{2}{u}$

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant