Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Express as a function of a DIFFERENT angle, 0^(@) <= theta < 360^(@). tan(174^(@)) tan(◻^(@))

Express as a function of a DIFFERENT angle, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} .\newlinetan⁡(174∘) \tan \left(174^{\circ}\right) \newlinetan⁡(□∘) \tan \left(\square^{\circ}\right)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find trigonometric ratios using reference anglesright chevron icon

Full solution

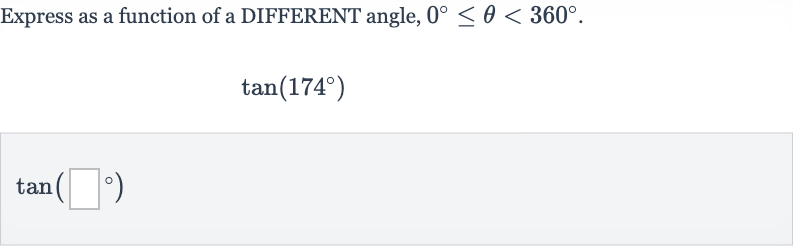
Q. Express as a function of a DIFFERENT angle, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} .\newlinetan⁡(174∘) \tan \left(174^{\circ}\right) \newlinetan⁡(□∘) \tan \left(\square^{\circ}\right)
  1. Understand Problem: Understand the problem and the range for θ\theta. We need to express tan⁡(174∘)\tan(174^\circ) in terms of a different angle that is within the specified range of 0∘0^\circ to 360∘360^\circ. Since 174∘174^\circ is already within this range, we need to find an equivalent angle that has the same tangent value but is not 174∘174^\circ itself.
  2. Find Reference Angle: Find the reference angle for 174°174°. The reference angle is the acute angle formed by the terminal side of the given angle and the x-axis. Since 174°174° is in the second quadrant, its reference angle is 180°−174°=6°180° - 174° = 6°.
  3. Determine Equivalent Angle: Determine the equivalent angle with the same tangent value.\newlineThe tangent function is positive in the first and third quadrants and negative in the second and fourth quadrants. Since 174∘174^\circ is in the second quadrant and we want a different angle, we can use the angle in the fourth quadrant that has the same reference angle, which is 360∘−6∘=354∘360^\circ - 6^\circ = 354^\circ.
  4. Express in terms of tan: Express tan⁡(174°)\tan(174°) in terms of tan⁡(354°)\tan(354°).\newlineSince tan⁡(θ)=tan⁡(θ+180°)\tan(\theta) = \tan(\theta + 180°) for all θ\theta, and 174°174° and 354°354° differ by 180°180°, we have tan⁡(174°)=tan⁡(354°)\tan(174°) = \tan(354°).

More problems from Find trigonometric ratios using reference angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 1 month ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (102)