Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Express as a function of a DIFFERENT angle, 0^(@) <= theta < 360^(@). sin(344^(@)) sin(◻^(@))

Express as a function of a DIFFERENT angle, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} .\newlinesin⁡(344∘) \sin \left(344^{\circ}\right) \newlinesin⁡(□∘) \sin \left(\square^{\circ}\right)

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Find trigonometric ratios using reference anglesright chevron icon

Full solution

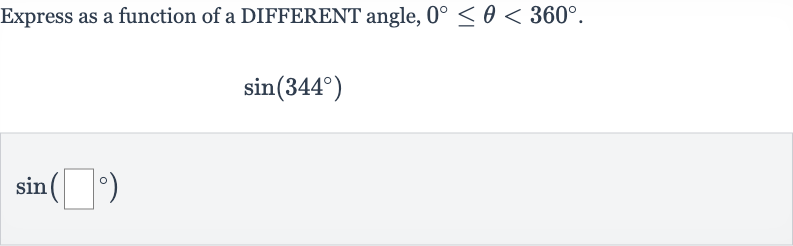
Q. Express as a function of a DIFFERENT angle, 0∘≤θ<360∘ 0^{\circ} \leq \theta<360^{\circ} .\newlinesin⁡(344∘) \sin \left(344^{\circ}\right) \newlinesin⁡(□∘) \sin \left(\square^{\circ}\right)
  1. Understand Period of Sine Function: Recognize that the sine function has a period of 360°360°, which means that sin⁡(θ)=sin⁡(θ+360°k)\sin(\theta) = \sin(\theta + 360°k), where kk is an integer. However, since we want to express sin⁡(344°)\sin(344°) as a function of a different angle within the range of 0°0° to 360°360°, we need to find an angle that is coterminal with 344°344° and falls within the specified range.
  2. Find Coterminal Angle: To find a coterminal angle that is within the range of 0∘0^\circ to 360∘360^\circ, we can subtract 360∘360^\circ from 344∘344^\circ if the angle is greater than 360∘360^\circ, or add 360∘360^\circ if the angle is less than 0∘0^\circ. Since 344∘344^\circ is less than 360∘360^\circ, we can find a coterminal angle by subtracting 344∘344^\circ from 360∘360^\circ.
  3. Calculate Coterminal Angle: Calculate the coterminal angle by subtracting 344∘344^\circ from 360∘360^\circ. \newline360∘−344∘=16∘360^\circ - 344^\circ = 16^\circ\newlineSo, sin⁡(344∘)\sin(344^\circ) is equivalent to sin⁡(360∘−16∘)\sin(360^\circ - 16^\circ), which is sin⁡(16∘)\sin(16^\circ) because sine is an odd function, and sin⁡(−θ)=−sin⁡(θ)\sin(-\theta) = -\sin(\theta).
  4. Express as Different Angle: Since sin⁡(344°)=sin⁡(16°)\sin(344°) = \sin(16°), we have expressed sin⁡(344°)\sin(344°) as a function of a different angle within the range of 0°0° to 360°360°.

More problems from Find trigonometric ratios using reference angles

Question
Find all solutions with 0∘≤θ≤180∘0^\circ \leq \theta \leq 180^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecos⁡(θ)=−1\cos(\theta) = -1\newline‾∘\underline{\hspace{2em}}^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Kimi's school is 1515 kilometers west of her house and 88 kilometers south of her friend Franklin's house. Every day, Kimi bicycles from her house to her school. After school, she bicycles from her school to Franklin's house. Before dinner, she bicycles home on a bike path that goes straight from Franklin's house to her own house. How far does Kimi bicycle each day?\newline_____\_\_\_\_\_ kilometers
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer as an integer or as a decimal rounded to the nearest hundredth.\newlinecos⁡35∘=\cos 35^\circ = __
Get tutor helpright-arrow

Posted 1 month ago

Question
Find all solutions with −90∘≤θ≤90∘-90^\circ \leq \theta \leq 90^\circ. Give the exact answer(s) in simplest form. If there are multiple answers, separate them with commas.\newlinecsc⁡(θ)=−1\csc(\theta) = -1\newline____ ∘\_\_\_\_\,^\circ
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecot⁡30∘=\cot 30^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
The terminal side of an angle θ\theta in standard position intersects the unit circle at (8485,1385)(\frac{84}{85}, \frac{13}{85}). What is cos⁡(θ)\cos(\theta)?\newlineWrite your answer in simplified, rationalized form.\newline______
Get tutor helpright-arrow

Posted 1 month ago

Question
−90∘<θ<90∘-90^\circ < \theta < 90^\circ. Find the value of θ\theta in degrees.\newlinetan⁡(θ)=0\tan(\theta) = 0\newlineWrite your answer in simplified, rationalized form. Do not round.\newlineθ=\theta = ____∘^\circ\newline
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecsc⁡60∘=\csc 60^\circ = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
θ\theta is an acute angle. Find the value of θ\theta in degrees.\newlinesec⁡(θ)=2\sec(\theta) = \sqrt{2}\newlineθ=\theta = ____°\degree
Get tutor helpright-arrow

Posted 1 month ago

Question
Evaluate. Write your answer in simplified, rationalized form. Do not round.\newlinecos⁡90∘=\cos 90^\circ = ____
Get tutor helpright-arrow

Posted 2 months ago

View all (102)