Full solution
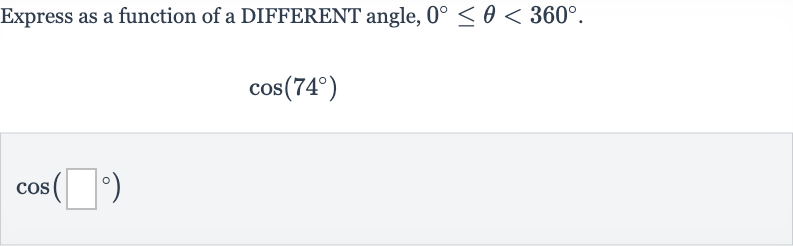
Q. Express as a function of a DIFFERENT angle, .
- Understand Co-function Identities: Understand the concept of co-function identities. Co-function identities relate the trigonometric functions of an angle to the trigonometric functions of its complement. The complement of an angle is . For cosine, the co-function identity is .
- Apply Co-function Identity: Apply the co-function identity to . Using the co-function identity, we can express as .
- Calculate Complement: Calculate the complement of . The complement of is .
- Write Final Expression: Write the final expression.Therefore, can be expressed as .
More problems from Sin, cos, and tan of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help