Full solution
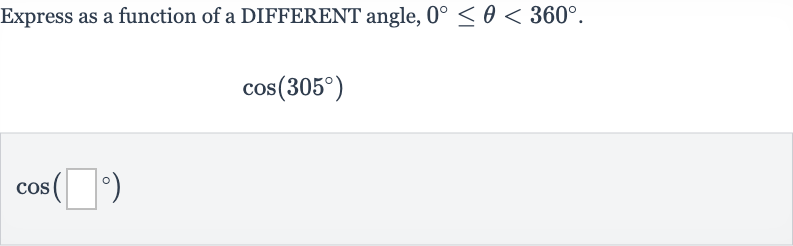
Q. Express as a function of a DIFFERENT angle, .
- Identify Reference Angle: Identify the reference angle for . The reference angle is the acute angle formed by the terminal side of the given angle and the x-axis. Since is in the fourth quadrant, we subtract it from to find the reference angle. Reference angle =
- Determine Cosine: Determine the cosine of the reference angle.Since cosine is positive in the fourth quadrant and the reference angle is , is equal to the cosine of its reference angle.
- Express as Different Angle: Express as a function of a different angle.We can use the symmetry properties of the cosine function to express in terms of a different angle. Since the cosine function is even, . Therefore, we can express as .
More problems from Find trigonometric ratios using reference angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help