Full solution
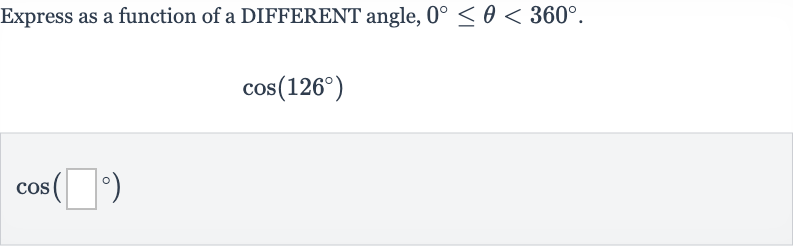
Q. Express as a function of a DIFFERENT angle, .
- Understand reference angles: Understand the concept of reference angles. A reference angle is the acute angle formed by the terminal side of an angle and the x-axis. It is always between and and is found by looking at the angle's position in relation to the nearest x-axis.
- Determine angle quadrant: Determine the quadrant in which the angle lies.The angle lies in the second quadrant, where the cosine function is negative.
- Find reference angle: Find the reference angle for .To find the reference angle, subtract the angle from because it is in the second quadrant.Reference angle =
- Express using reference angle: Express using its reference angle.Since cosine is negative in the second quadrant and the reference angle is , we can express as .
More problems from Sin, cos, and tan of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help