Full solution
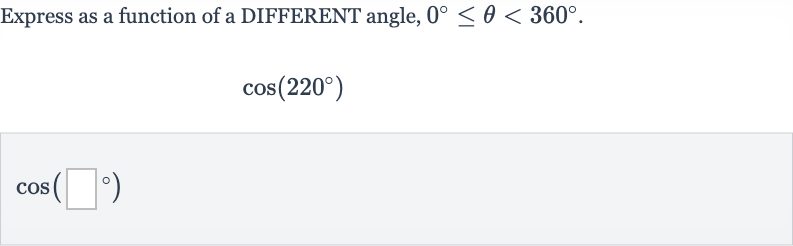
Q. Express as a function of a DIFFERENT angle, .
- Understand reference angles: Understand the concept of reference angles. A reference angle is the acute angle formed by the terminal side of an angle and the x-axis. It is always between and and is found by looking at the angle's location in the standard position and determining how far it is from the nearest x-axis.
- Find reference angle for : Find the reference angle for . Since is in the third quadrant, we subtract it from to find the reference angle. Reference angle =
- Determine cosine sign in third quadrant: Determine the sign of the cosine function in the third quadrant.In the third quadrant, both the and coordinates are negative, so the cosine function, which corresponds to the -coordinate, is negative.
- Express with reference angle: Express in terms of the reference angle.Since the cosine function is negative in the third quadrant and the reference angle is , we can write:
- Verify reference angle within range: Verify that the reference angle is within the specified range.The reference angle is within the range 0^\circ \leq \theta < 360^\circ, so our expression is valid.
More problems from Sin, cos, and tan of special angles
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
Question
. Find the value of in degrees.Write your answer in simplified, rationalized form. Do not round.____
Get tutor helpQuestionGet tutor help