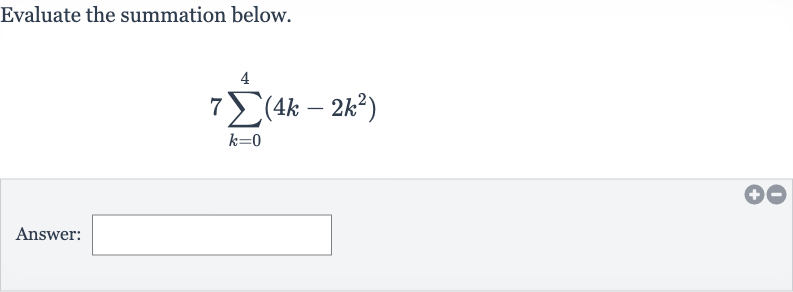AI tutor
Full solution
Q. Evaluate the summation below.Answer:
- Evaluate Series: We need to evaluate the summation of the series given by the expression times the sum from to of . We will do this by calculating the sum term by term and then multiplying by .
- Calculate Terms: First, let's calculate the sum without the factor of . We will substitute and into the expression and find the sum of these values.
- Calculate Sum: For : . For : . For : . For : . For : . Now, we add these values together to get the sum.
- Multiply by : The sum is .
- Multiply by : The sum is .Now, we multiply this sum by to get the final answer..