AI tutor
Full solution
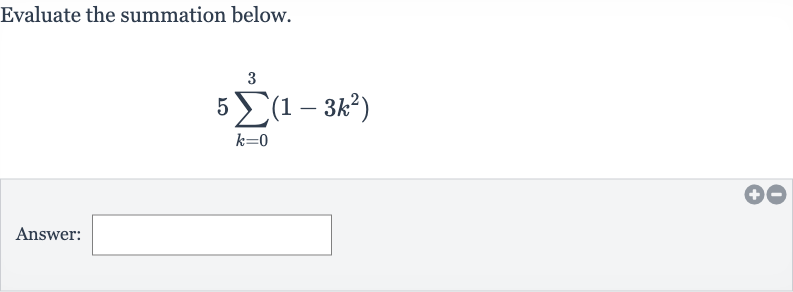
Q. Evaluate the summation below.Answer:
- Write Terms Explicitly: Write out the terms of the series explicitly.The series is times the sum from to of . This means we need to calculate the value of for each from to and then multiply the sum of these values by .
- Calculate Terms: Calculate the terms of the series.For : For : For : For :
- Sum Terms: Sum the terms of the series.The sum of the terms from to is .This sum is .
- Multiply by : Multiply the sum by . The final step is to multiply the sum of the series by . .