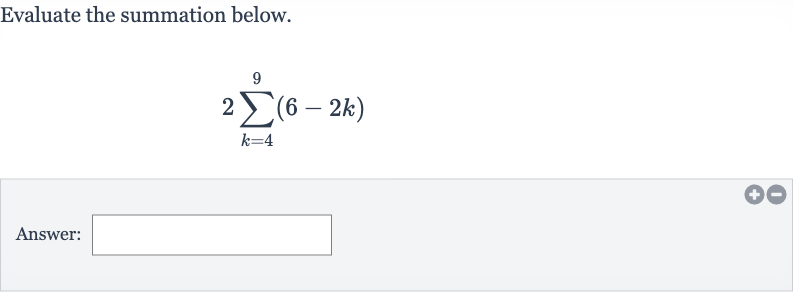
Evaluate the summation below. 2sum_(k=4)^(9)(6-2k) Answer:

Question

Evaluate the summation below.  2sum_(k=4)^(9)(6-2k) Answer:

Bytelearn · Accepted Answer

Multiply by 2: Write down the expression inside the summation and multiply it by 2 as indicated by the problem. The expression inside the summation is (6 - 2k), and we need to multiply it by 2, which gives us 2(6 - 2k) = 12 - 4k.Apply summation to terms: Apply the summation to each term in the expression 12 - 4k from k=4 to k=9. We need to sum both 12 and -4k separately over the range of k from 4 to 9.Evaluate constant term: Evaluate the constant term 12 in the summation. Since 12 is a constant, the summation of 12 from k=4 to k=9 is simply 12 multiplied by the number of terms, which is 9 - 4 + 1 = 6. So, sum_(k=4)^(9)12 = 12 * 6 = 72.Evaluate variable term: Evaluate the variable term -4k in the summation. We use the formula for the sum of the first n integers, sum_(k=1)^(n)k = n(n+1)/2, but we need to adjust it for the range from 4 to 9. First, find the sum from 1 to 9, then subtract the sum from 1 to 3. sum_(k=1)^(9)k = 9(9+1)/2 = 45. sum_(k=1)^(3)k = 3(3+1)/2 = 6. Now subtract the two sums: 45 - 6 = 39. Finally, multiply by -4 to account for the -4k term: -4 * 39 = -156.Combine results: Combine the results from Step 3 and Step 4 to find the total sum. Total sum = sum of constant terms + sum of variable terms = 72 - 156 = -84.

Evaluate the summation below. $\newline$ $2 \sum_{k=4}^{9}(6-2 k)$ $\newline$ Answer:

Full solution

More problems from Sum of finite series starts from 1

Related topics

Evaluate the summation below.\newline2∑k=49(6−2k) 2 \sum_{k=4}^{9}(6-2 k) 2k=4∑9​(6−2k)\newlineAnswer:

Evaluate the summation below. $\newline$ $2 \sum_{k=4}^{9}(6-2 k)$ $\newline$ Answer: