Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

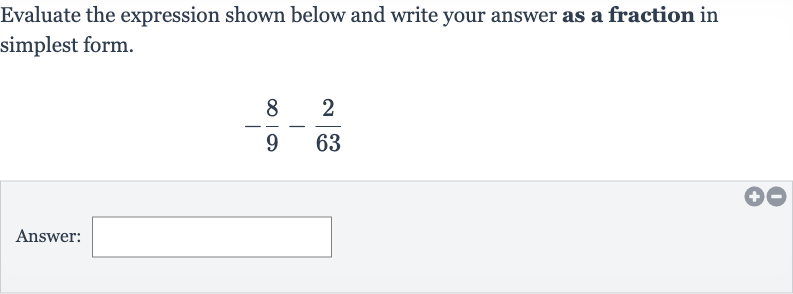
$Evaluate the expression shown below and write your answer as a fraction in simplest form. -(8)/(9)-(2)/(63) Answer:$

Evaluate the expression shown below and write your answer as a fraction in simplest form. $\newline$ $-\frac{8}{9}-\frac{2}{63}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Multiplication with rational exponents

Full solution

Q. Evaluate the expression shown below and write your answer as a fraction in simplest form.

\newline

-\frac{8}{9}-\frac{2}{63}

\newline

Answer:

Find Common Denominator: Identify a common denominator for the fractions. $\newline$ The fractions $-\frac{8}{9}$ and $-\frac{2}{63}$ have different denominators. To combine them, we need to find a common denominator. The least common multiple (LCM) of $9$ and $63$ is $63$ .
Convert Fractions: Convert the fractions to have the common denominator. $\newline$ The first fraction $-\frac{8}{9}$ needs to be converted to have a denominator of $63$ . We do this by multiplying both the numerator and the denominator by $7$ (since $63$ is $7$ times $9$ ). $\newline$ So, $-\frac{8}{9}$ becomes $-\frac{8\times 7}{9\times 7} = -\frac{56}{63}$ . $\newline$ The second fraction $-\frac{2}{63}$ already has the common denominator, so it remains unchanged.
Combine Fractions: Combine the fractions. $\newline$ Now that both fractions have the same denominator, we can combine them by adding their numerators together. $\newline$ So, $-\frac{56}{63}$ - $\frac{2}{63}$ = $\frac{-56 - 2}{63}$ = $-\frac{58}{63}$ .
Simplify Result: Simplify the fraction, if possible. $\newline$ The fraction $-\frac{58}{63}$ cannot be simplified further because $58$ and $63$ do not have any common factors other than $1$ .

More problems from Multiplication with rational exponents

Question

\newline

81^{\frac{1}{2}}

\newline

Posted 9 months ago

Question

\newline

(-32)^{1/5}

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

(2r^{\frac{1}{3}})^8

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 5 months ago

Question

Simplify. Assume all variables are positive.

\newline

v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 5 months ago

Question

\newline

1^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}

\newline

Posted 5 months ago

Question

\newline

32^{(-1/5)}

Posted 7 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 9 months ago

Question

Simplify. Assume all variables are positive.

\newline

(27x)^{\frac{2}{3}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

Posted 8 months ago

Question

Simplify. Assume all variables are positive.

\newline

\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}

\newline

\newline

Write your answer in the form

A

\frac{A}{B}

A

B

are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.

\newline

\newline

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant