Resources

Testimonials

Plans

Resources

Testimonials

Plans

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

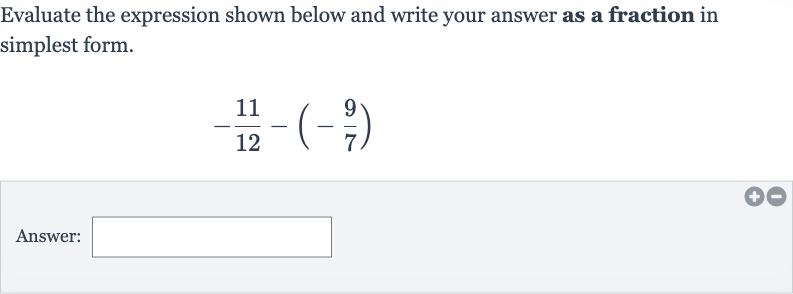
$Evaluate the expression shown below and write your answer as a fraction in simplest form. -(11)/(12)-(-(9)/(7)) Answer:$

Evaluate the expression shown below and write your answer as a fraction in simplest form. $\newline$ $-\frac{11}{12}-\left(-\frac{9}{7}\right)$ $\newline$ Answer:

View step-by-step help

Home

Math Problems

Algebra 1

Multiplication with rational exponents

Full solution

Q. Evaluate the expression shown below and write your answer as a fraction in simplest form.

\newline

-\frac{11}{12}-\left(-\frac{9}{7}\right)

\newline

Answer:

Understand and Identify Operations: Understand the expression and identify the operations to be performed. We have the expression $-\left(\frac{11}{12}\right) - \left(-\left(\frac{9}{7}\right)\right)$ . This expression involves two operations: subtraction and negation (the negative sign in front of the fractions).
Remove Double Negative: Simplify the expression by removing the double negative. $\newline$ The double negative in the expression $-(\frac{11}{12}) - (-(\frac{9}{7}))$ turns the second term into a positive, so the expression becomes: $\newline$ $-(\frac{11}{12}) + (\frac{9}{7})$
Find Common Denominator: Find a common denominator for the fractions. $\newline$ The denominators are $12$ and $7$ , which are co-prime (they have no common factors other than $1$ ). Therefore, the common denominator will be the product of $12$ and $7$ , which is $84$ .
Convert to Common Denominator: Convert each fraction to an equivalent fraction with the common denominator. $\newline$ For the first fraction: $\newline$ $-\frac{11}{12} = -\frac{11 \times 7}{12 \times 7} = -\frac{77}{84}$ $\newline$ For the second fraction: $\newline$ $\frac{9}{7} = \frac{9 \times 12}{7 \times 12} = \frac{108}{84}$
Add Fractions: Add the fractions with the common denominator. $\newline$ Now we add the two fractions: $\newline$ $-\frac{77}{84}$ + $\frac{108}{84}$ = $\frac{108}{84}$ - $\frac{77}{84}$ = $\frac{108 - 77}{84}$ = $\frac{31}{84}$
Check for Simplification: Check if the resulting fraction can be simplified. $\newline$ The numerator $31$ and the denominator $84$ have no common factors other than $1$ , so the fraction is already in its simplest form.