Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

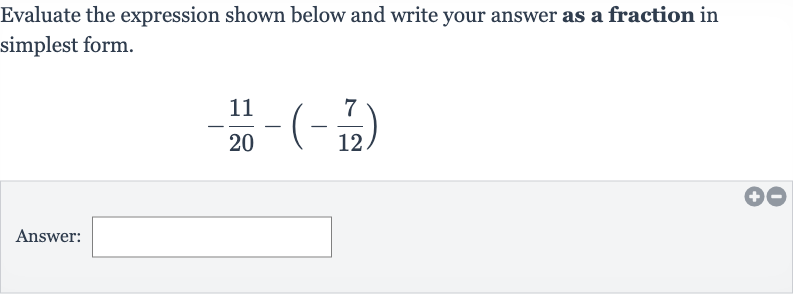
Evaluate the expression shown below and write your answer as a fraction in simplest form. -(11)/(20)-(-(7)/(12)) Answer:

Evaluate the expression shown below and write your answer as a fraction in simplest form.\newline−1120−(−712) -\frac{11}{20}-\left(-\frac{7}{12}\right) \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Multiplication with rational exponentsright chevron icon

Full solution

Q. Evaluate the expression shown below and write your answer as a fraction in simplest form.\newline−1120−(−712) -\frac{11}{20}-\left(-\frac{7}{12}\right) \newlineAnswer:
  1. Understand Operations: Understand the expression and identify the operations to be performed. We need to subtract the second fraction from the first one, and also take into account the negative signs.
  2. Simplify Expression: Simplify the expression by removing the double negative.\newlineThe double negative in the expression −(1120)−(−(712)) -(\frac{11}{20}) - (-(\frac{7}{12})) turns the second term into a positive, so the expression becomes:\newline−(1120)+(712) -(\frac{11}{20}) + (\frac{7}{12})
  3. Find Common Denominator: Find a common denominator for the fractions.\newlineThe least common multiple (LCM) of 2020 and 1212 is 6060, so we will convert both fractions to have a denominator of 6060.
  4. Convert First Fraction: Convert the first fraction to have a denominator of 6060.\newlineTo convert 1120\frac{11}{20} to a fraction with a denominator of 6060, multiply both the numerator and the denominator by 33:\newline(11×3)/(20×3)=3360\left(11 \times 3\right) / \left(20 \times 3\right) = \frac{33}{60}
  5. Convert Second Fraction: Convert the second fraction to have a denominator of 6060. To convert 712\frac{7}{12} to a fraction with a denominator of 6060, multiply both the numerator and the denominator by 55: (7×5)/(12×5)=3560\left(7 \times 5\right) / \left(12 \times 5\right) = \frac{35}{60}
  6. Combine Fractions: Combine the fractions with the common denominator.\newlineNow that both fractions have the same denominator, we can combine them:\newline−3360+3560-\frac{33}{60} + \frac{35}{60}
  7. Perform Addition: Perform the addition of the fractions.\newlineSubtract the numerators and keep the common denominator:\newline−3360-\frac{33}{60} + 3560\frac{35}{60} = 3560\frac{35}{60} - 3360\frac{33}{60} = 35−3360\frac{35 - 33}{60} = 260\frac{2}{60}
  8. Simplify Resulting Fraction: Simplify the resulting fraction.\newlineThe fraction 260\frac{2}{60} can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 22:\newline(22)/(602)=130(\frac{2}{2}) / (\frac{60}{2}) = \frac{1}{30}

More problems from Multiplication with rational exponents

Question
Simplify.\newline811281^{\frac{1}{2}}\newline_____________
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify.\newline(−32)1/5(-32)^{1/5}\newline______
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newlinew43w73\frac{w^{\frac{4}{3}}}{w^{\frac{7}{3}}}\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newline(2r13)8(2r^{\frac{1}{3}})^8\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. Assume all variables are positive.\newlinev74⋅v94v^{\frac{7}{4}} \cdot v^{\frac{9}{4}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify.\newline114⋅1141^{\frac{1}{4}} \cdot 1^{\frac{1}{4}}\newline______
Get tutor helpright-arrow

Posted 5 months ago

Question
Simplify. \newline32(−1/5)32^{(-1/5)}
Get tutor helpright-arrow

Posted 7 months ago

Question
Simplify. Assume all variables are positive.\newlinew32w52\frac{w^{\frac{3}{2}}}{w^{\frac{5}{2}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 9 months ago

Question
Simplify. Assume all variables are positive.\newline(27x)23(27x)^{\frac{2}{3}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______
Get tutor helpright-arrow

Posted 8 months ago

Question
Simplify. Assume all variables are positive.\newlinex14x114\frac{x^{\frac{1}{4}}}{x^{\frac{11}{4}}}\newline\newlineWrite your answer in the form AA or AB\frac{A}{B}, where AA and BB are constants or variable expressions that have no variables in common. All exponents in your answer should be positive.\newline______\newline
Get tutor helpright-arrow

Posted 7 months ago

View all (744)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant