Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

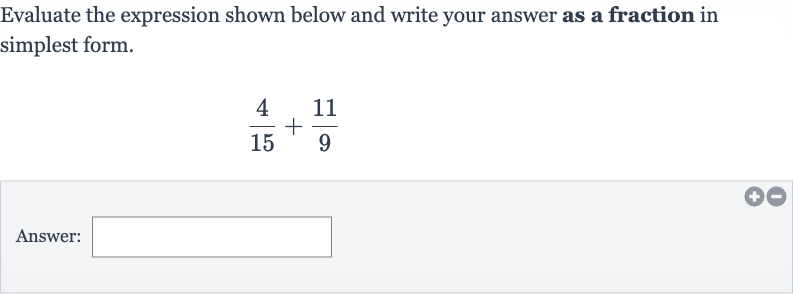
$Evaluate the expression shown below and write your answer as a fraction in simplest form. (4)/(15)+(11)/(9) Answer:$

Evaluate the expression shown below and write your answer as a fraction in simplest form. $\newline$ $\frac{4}{15}+\frac{11}{9}$ $\newline$ Answer:

View step-by-step help

View step-by-step help

Roots of rational numbers

Full solution

Q. Evaluate the expression shown below and write your answer as a fraction in simplest form.

\newline

\frac{4}{15}+\frac{11}{9}

\newline

Answer:

Find Common Denominator: To add two fractions, we need to find a common denominator. The denominators here are $15$ and $9$ . The least common multiple (LCM) of $15$ and $9$ is $45$ .
Convert to Equivalent Fractions: Now we convert each fraction to an equivalent fraction with the denominator of $45$ . For the first fraction, $\frac{4}{15}$ , we multiply both the numerator and the denominator by $3$ to get $\left(\frac{4 \times 3}{15 \times 3}\right) = \frac{12}{45}$ . For the second fraction, $\frac{11}{9}$ , we multiply both the numerator and the denominator by $5$ to get $\left(\frac{11 \times 5}{9 \times 5}\right) = \frac{55}{45}$ .
Add Fractions: Next, we add the two fractions with the common denominator: $\frac{12}{45} + \frac{55}{45} = \left(12 + 55\right) / 45 = \frac{67}{45}$ .
Simplify Fraction: The fraction $\frac{67}{45}$ is already in its simplest form because $67$ and $45$ have no common factors other than $1$ .

More problems from Roots of rational numbers

Question

Find the real-number root.

\newline

\sqrt{16}

\newline

\newline

Write your answer in simplified form.

\newline

\_\_\_\_

Posted 9 months ago

Question

Find the real-number root.

\newline

\sqrt{\frac{9}{16}}

\newline

Simplify your answer and write it as a decimal or as a proper or improper fraction.

\newline

\_\_\_\_\_

Posted 9 months ago

Question

Find the real-number root using a calculator. Round your answer to the nearest thousandth.

\newline

\newline

Posted 9 months ago

Question

Multiply. Write your answer in simplest form.

\newline

\sqrt{273} \times \sqrt{42}

\newline

Posted 7 months ago

Question

\newline

\sqrt{\frac{63}{4}}

\newline

Posted 9 months ago

Question

Simplify. Rationalize the denominator.

\newline

\frac{-4}{9 - \sqrt{2}}

\newline

Posted 9 months ago

Question

z

\newline

16 = \sqrt{z}

\newline

z =

Posted 9 months ago

Question

Simplify the radical expression.

\sqrt{14x^{14}}

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

Posted 9 months ago

Question

Simplify the radical expression.

\newline

\sqrt{12x^{12}}

\newline

Write your answer in the form

A

\sqrt{B}

A\sqrt{B}

A

B

are constants or expressions in

x

. Use at most one radical in your answer, and at most one absolute value symbol in your expression for

A

\newline

\underline{\hspace{3cm}}

Posted 9 months ago

Question

What is the value of

\sin \left(\frac{5 \pi}{6}\right) ?

\newline

1

\newline

-\frac{\sqrt{3}}{2}

\newline

-\frac{\sqrt{2}}{2}

\newline

\frac{1}{2}

\newline

150

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant