AI tutor
Full solution
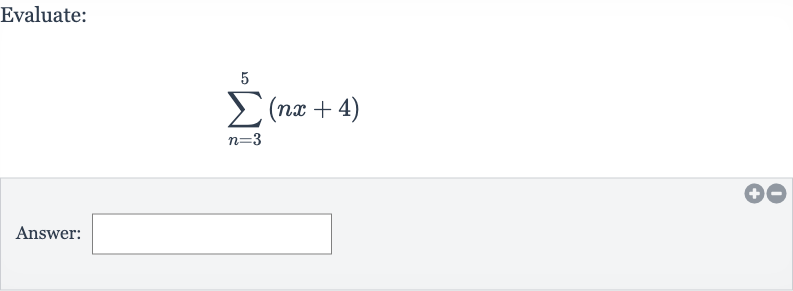
Q. Evaluate:Answer:
- Understand the problem: Understand the problem We need to evaluate the sum of the expression for ranging from to .
- Write out the terms: Write out the terms of the sumThe sum from to of means we need to calculate .
- Evaluate each term: Evaluate each termFirst term when : Second term when : Third term when :
- Add the terms together: Add the terms togetherNow we add the terms we found in Step together:
- Combine like terms: Combine like termsCombine the terms: Combine the constant terms: So,
More problems from Evaluate rational expressions II
QuestionGet tutor help